Blog
Braiding, pt. 1: The question
2016-06-29
Since Electromagnetic Field 2014, I have been slowly making
progress on a recreational math problem about braiding. In this blog post, I
will show you the type of braid I am interested in and present the problem.
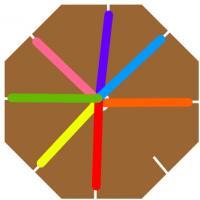
Making an (8,3) braid
To make what I will later refer to as an (8,3) braid, you will need:
- 7 lengths of coloured wool, approx 50cm each
- Cardboard
- Scissors
- A pencil
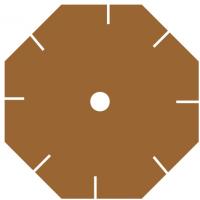
First, cut an octagon from the cardboard. The easiest way to do this is
to start with a rectangle, then cut its corners off.
![](javascript:showlimage("braid_in1.png"))
Next, use the pencil to punch a hole in the middle of your octagon and
cut a small slit in each face of the octagon.
![](javascript:showlimage("braid_in2.png"))
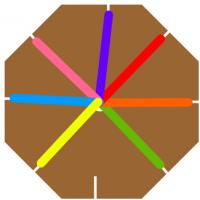
Now, tie the ends of your wool together, and put them through the hole.
pull each strand of wool into one of the slits.
![](javascript:showlimage("braid_in3.png"))
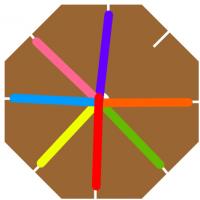
Now you are ready to make a braid. Starting from the empty slit, count around
to the third strand of will. Pull this out of its slit then into the empty slit.
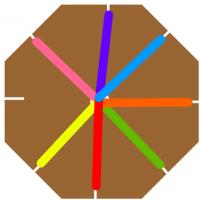
Then repeat this starting at the newly empty slit each time. After a short time,
a braid should form through the hole in the cardboard.
![](javascript:showlimage("braid_in-m1.png"))
![](javascript:showlimage("braid_in-m2.png"))
![](javascript:showlimage("braid_in-m3.png"))
The problem
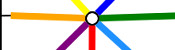
I call the braid you have just made the (8,3) braid, as there are 8 slits and
you move the 3rd strand each time. After I first made on of these braid, I began
to wonder what was special about 8 and 3 to make this braid work, and for what
other numbers \(a\) and \(b\) the (\(a\),\(b\)) would work.
In my next blog post, I will give two conditions on \(a\) and \(b\) that cause
the braid to fail. Before you read that, I recommend having a go at the problem
yourself. To help you on your way, I am compiling a list of braids that are known
to work or fail at mscroggs.co.uk/braiding. Good luck!
×2 ×1 ×1 ×1 ×1(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2020-04-20
@no: yes, although rectangles work surprisingly wellMatthew
×1 ×1 ×1 ×1 Add a Comment