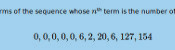Blog
2023-04-12
If, like me, you grew up in the 90s, then one of your earliest experiences of programming was
probably using Logo. In Logo, you use various commands to move a "turtle" around the screen. As the turtle moves,
it can draw lines. I have a very strong memory from early secondary school of spending a few maths
lessons in the computer room writing Logo programs to draw isometric houses.
If you read this blog regularly, you'll probably have noticed that I'm a fan of the game
Asteroids. Over the last few weeks, I've been working on Logo Asteroids,
a version of Asteroids where you control your spaceship using Logo commands. You can play this game
at mscroggs.co.uk/logo.
If you've not used Logo before, or if it's been so long since you have that you've forgotten the commands,
this blog post will guide you through how to get started. If you're confident in your Logo skills,
you might still want to scroll to the end of this post, where I share some custom Logo commands that you
might find helpful.
The game's source code is available on Github;
you can also use the GitHub issue tracker to report bugs and make feature requests.
Moving the turtle
If you're starting out in Logo, the first thing you'll want to do is move the turtle.
You can move it forwards or backwards using the commands fd or
bk followed by a number of pixels:
Logo
fd 100
bk 75
To change the direction in which the turtle is facing, you can use the command rt (right)
or lt (left) followed by an angle in degrees:
Logo
rt 90
lt 45
You can also chain together multiple commands on a single line like this:
Logo
fd 100 rt 90 fd 100 lt 90
By default, a line is drawn whenever the turtle moves forward or backwards. You can stop lines from being
drawn by running the command pu (pen up). To start drawing again, run
pd (pen down). If you want to make the game needlessly harder for yourself, you can use the command ht (hide turtle). To make the game easier again, run st (show turtle).
In a normal Logo program, the lines that you draw will stay there until you clear the screen (cs). In Logo Asteroids, the lines will only be visible for a limited amount
of time, and the asteroids will bounce off them while they are visible. To prevent too many lines from being drawn too quickly,
the turtle can move a maximum of 1000 pixels in a single command (or chain of commands).
Special commands for Logo Asteroids
As well as the Logo commands, there are some commands I have included that are specific to Logo
Asteroids. These are:
Logo
start
fire
help
The command start will start the game. You'll need to run this before you can run any other commands. You'll also need to run it to start the game again if you
run out of lives.
The command fire will fire at the asteroids. This command can be run
a maximum of 10 times by a single chain of commands.
The command help will show details of all the available commands below the game.
Defining your own subroutines
If you write some Logo commands that you want to use lots of times, use can use the to command to define a subroutine.
For example, the following code defined a command called square that will draw a square of side length 50.
Logo
to square fd 50 rt 90 fd 50 rt 90 fd 50 rt 90 fd 50 rt 90 end
The subroutine can then be used by running:
Logo
square
The square subroutine can be simplified by using the repeat command:
Logo
to square repeat 4 [fd 50 rt 90] end
... or it could be made to take a side length as input:
Logo
to square :side repeat 4 [fd :side rt 90] end
This updated version of the square subroutine can then be used by running:
Logo
square 50
square 100
square 125
Helpful subroutines for Logo Asteroids
To help you get going with Logo Asteroids, I've written a few subroutines that you might find helful. See if you
can work out what they do before running them.
Logo
to burst repeat 10 [fire rt 36] end
to protect pu fd 30 pd rt 135 repeat 4 [fd 30 * sqrt 2 rt 90] lt 135 pu bk 30 pd end
to multifire rt 10 repeat 10 [fire lt 2] rt 10 end
If you write your own helpful subroutine, share it in the comments below. You can put <logo> and </logo> HTML tags around your subroutine to make it display more nicely in your comment.
To end this blog post, here's one final subroutine for you to try out:
Logo
to house pu setxy 400 225 seth 0 pd lt 30 fd 40 lt 60 fd 40 lt 120 fd 40 lt 60 fd 40 rt 120 fd 50 rt 60 fd 40 rt 120 fd 50 setxy 400 + 20 * cos 30 155 rt 180 fd 50 setxy 400 - 50 * cos 30 160 pu setxy 400 + 20 * cos 30 155 pd setxy 400 + 40 * cos 30 165 pu setxy 400 225 lt 60 pd fd 50 rt 60 fd 50 rt 120 fd 50 pu rt 60 fd 20 pd lt 120 fd 20 rt 120 fd 10 rt 60 fd 20 rt 60 fd 50 pu rt 60 fd 10 pd rt 120 fd 50 ht end
×5 ×5 ×3 ×3 ×5(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2023-04-13
Very cool! Here's a combination of your "burst" and "protect" subroutines:
to f pu sety 195 setx 390 pd repeat 10 [fire fd 20 rt 36] pu home end
Aaron
×4 ×3 ×4 ×4 ×4 I didn't include this one in the blog post, but here's a bonus fun command:
×4 ×4 ×4 ×4 ×5
to randwalk repeat 100 [rt random 360 fd 10] end
Matthew
×4 ×4 ×4 ×4 ×5 Add a Comment
2022-12-29
This is the 100th blog post on this website!
But if I hadn't pointed this out,
you might not have noticed: the URL of the page is mscroggs.co.uk/blog/99 and not mscroggs.co.uk/blog/100.
This is a great example of an off-by-one error.
Off-by-one errors are one of the most common errors made when programming and elsewhere, and this is an excellent opportunity to blog about them.
Fence posts and fence panels
Imagine you want to make a straight fence that is 50m long. Each fencing panel is 2m long.
How many fence posts will you need?
Have a quick think about this before reading on.
If you're currently thinking about the number 25, then you've just made an off-by-one error.
The easiest way to see why is to think about some shorter fences.
If you want to make a fence that's 2m long, then you'll need just one fence panel. But one fence
post will not be enough: you'll need a second post to put at the other end of the fence panel.
If you want to make a 4m long fence, you'll need a post before the first panel, a post between
the two panels, and a post after the second panel: that's three posts in total.
In general, you'll always need one more fence post than panel, as you need a fence post
at the start of each panel and an extra post at the end of the final panel.
(Unless, of course, you're building a fence that is a closed loop.)
![](javascript:showlimage("fenceposts.png"))
This fence has 4 fence panels but 5 fence posts
This fence post/fence panel issue appears surprisingly often, and can make counting things
quite difficult. For example, the first blog post
on this website was posted in 2012: ten years ago. But if you count the number of years listed in the
archive there are 11 years. If you release an issue of a magazine once a year, then issue 11 (not issue 10) will
be the issue released 10 years after you start not issue 10. If, like Chalkdust,
you release issues two times a year, issue 21 (not issue 20) will be the 10 year issue.
Half-open intervals
An interval is called closed if it includes its starting and ending point, and open if it
doesn't include them. A half-open interval includes one end point and not the other.
Using half-open intervals makes counting things less difficult: including one endpoint but not the other is a bit like ignoring
the final (or first) fence post so that there are the same number of post and panels.
In Python, the range function includes the first number but not the last
(this is the sensible choice as including the final number and not the first would be very confusing).
range(5, 8) includes the numbers 5, 6, and 7 (but not 8).
By excluding the final number, the number of numbers in a range
will be equal to the difference between the two input numbers.
Excluding the final item so that the number of items in a range is equal to the difference between the start and end is a great way to
reduce opportunities for off-by-one errors, and isn't too hard to get used to.
Why start at 0?
We've seen a couple of causes of off-by-one errors, but we've not yet seen why this page's URL
contains 99 rather than 100. This is because the numbering of blog posts started at zero.
But why is it a sensible choice to start at 0?
Using a half-open range, the first \(n\) numbers starting at 1 would be range(1, n + 1); the first \(n\) numbers starting at 0 on the other hand
would be range(0, n). The second option is neater, as you don't have to add one to the final number; the first option opens up more opportunities for
off-by-one errors.
This is one of the reasons why Python and many other programming languages start their numbering from 0.
Why doesn't everyone start at 0?
Starting at 0 and using half-open intervals to represent ranges of integers seem like good ways to help people avoid making off-by-one errors, but this choice is not perfect.
If you want to write a range of numbers from 1 to 8 inclusive using this convention, you would have to write range(1, 9):
forgetting to add one to the final number in this situation is another source of off-by-one errors.
It's also more natural to many people to start counting from 1, so some programming languages choose different conventions. The following table sums up the different possible
conventions, which desirable properties they have, and which languages use them.
| Convenction | Languages using this convention | Length of range is difference between endpoints | range(START, n) contains \(n\) numbers | range(START, n) contains START | range(START, n) contains \(n\) |
| START=0, range includes first endpoint only | Python, Javascript, PHP, Rust, C, C++ | ✓ | ✓ | ✓ | ✗ |
| START=0, range includes last endpoint only | ✓ | ✓ | ✗ | ✓ | |
| START=0, range includes both endpoints | ✗ | ✗ | ✓ | ✓ | |
| START=0, range includes neither endpoint | ✗ | ✗ | ✗ | ✗ | |
| START=1, range includes first endpoint only | ✓ | ✗ | ✓ | ✗ | |
| START=1, range includes last endpoint only | ✓ | ✗ | ✗ | ✓ | |
| START=1, range includes both endpoints | Matlab, Julia, Fortran | ✗ | ✓ | ✓ | ✓ |
| START=1, range includes neither endpoint | ✗ | ✗ | ✗ | ✗ |
(I don't know of any languages that use any of the other conventions, but if you have please let me know in the comments below and I'll add them.)
None of the conventions manages to remove all the possible sources of confusion, so it looks like off-by-one errors are here to stay.
×1 (Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Hi!!!
Love your blog posts!
They make me get out of bed in the morning.
Just wanted to show my appreciation.
Cheers.×1
Love your blog posts!
They make me get out of bed in the morning.
Just wanted to show my appreciation.
Cheers.
Anonymous#3728
×1 Add a Comment
2022-02-26
Surprisingly often, people ask me how they can build their own copy of MENACE. If you've been thinking that you'd love your own matchbox-powered machine learning computer but haven't got round to asking me about it yet, then this blog post is just what you're looking for.
Matchboxes
Before building MENACE, you'll need to get hold of 304 matchboxes (plus a few spares in case one gets lost or falls apart). I used these craft matchboxes: they don't have the best build quality, but they're good enough.
304 positions
The positions you need to glue onto the front of the matchboxes can be downloaded from this GitHub repository (first move boxes, third move boxes, fifth move boxes, seventh move boxes). These are sized to fit on matchboxes that have 15mm by 35mm fronts.
I printed each pdf on differently coloured paper to make it easier to sort the matchboxes after getting them out of their box.
If you get differently sized matchboxes, the code used the generate the PDFs is in the same GitHub repository (you'll need to modify these lines). Alternatively, feel free to drop me an email and I will happily adjust the sizes for you and send you the updated PDFs.
Glue
I used PVA glue to stick the positions onto the matchboxes. The printable PDFs have extra tabs of paper above and below the postions that can be glued in to the bottom and inside of the matchbox tray to hold it more securely.
Gluing the positions onto the matchboxes was the most time consuming part of building my copy of MENACE, largely due to having to wait for the glue to dry on a set of matchboxes before I had space for the next batch of them to dry.
Beads
Once you've glued pictures of noughts and crosses positions to 304 matchboxes, you'll need to put coloured beads into each matchbox. For this, I used a large tub of Hama beads (that tub contained orders of magnitude more beads than I needed).
A nice side effect of using Hama beads is that they're designed to be ironed together so making a key to show which colour corresponds to each position is very easy.
I typically start the boxes off with 8 beads of each colour in the first move box, 4 of each colour in the third move boxes, 2 of each in the fifth move boxes, and one of each in the seventh move boxes.
Once you've filled all your matchboxes with the correct number of beads, you're ready to play yout first game against MENACE. I'd love to hear how you get on.
And once you're bored of playing noughts and crosses against your matchboxes, why not build a machine that learns to play Hexapawn, Connect 4, Chess or Go? Or one that plays Nim?
Edit: Added link to the printable pdfs of the positions needed for Hexapawn, made by Dan Whitman.
×9 ×6 ×5 ×6 ×7(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Interesting.
Could try a same kind of thing using playing card deck(s)? A(=1)-2-3 4-5-6 7-8-9 maybe 3 decks with different colours on their backs.×3 ×3 ×3 ×3 ×2
Could try a same kind of thing using playing card deck(s)? A(=1)-2-3 4-5-6 7-8-9 maybe 3 decks with different colours on their backs.
Willem
×3 ×3 ×3 ×3 ×2 I also read the Martin Gardner article way back when and had two matchbox machines (actually with envelopes instead of matchboxes) play Nim against each other. I don't remember all the details now, except that it got to the point where one would make the first move and the other would immediately resign.×5 ×2 ×2 ×2 ×2
Tim Lewis
×5 ×2 ×2 ×2 ×2 I made a matchbox machine that learns to play 3x3 Nim almost 50 years ago. I still have it. (Based on Martin Gardner's article)
×7 ×4 ×2 ×2 ×3
Tony
×7 ×4 ×2 ×2 ×3 Add a Comment
2019-12-27
In tonight's Royal Institution Christmas lecture,
Hannah Fry and Matt Parker demonstrated how machine learning works using MENACE.
The copy of MENACE that appeared in the lecture was build and trained by me. During the training, I logged all the moved made by MENACE and the humans playing against them, and using this data I have
created some visualisations of the machine's learning.
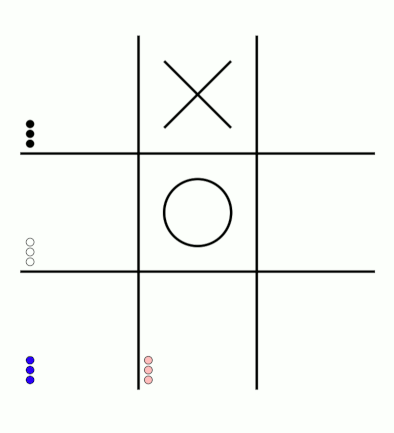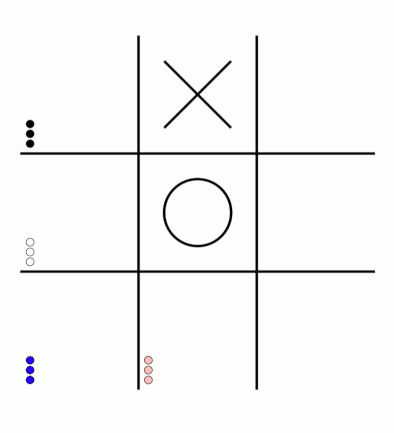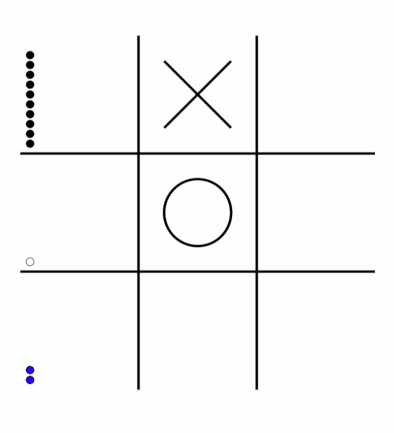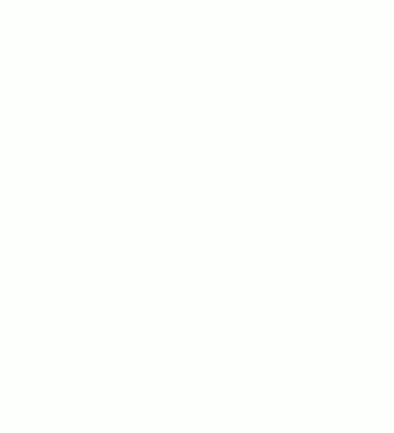
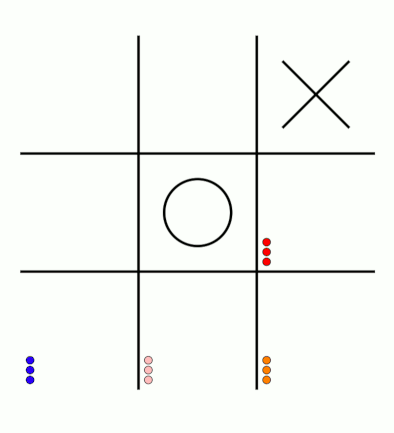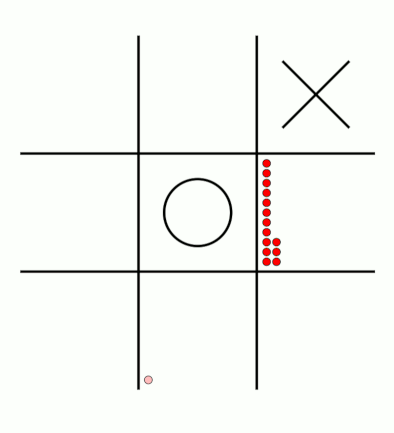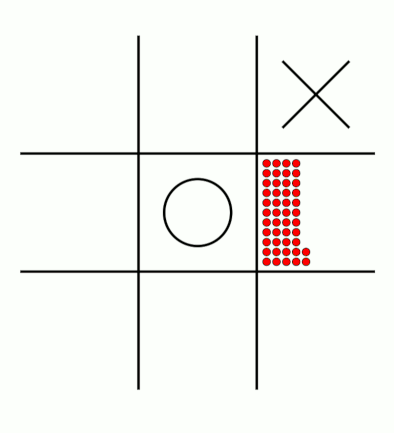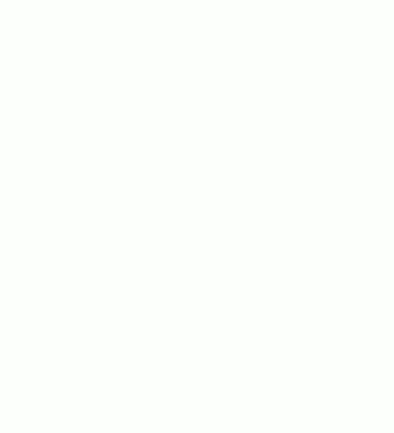
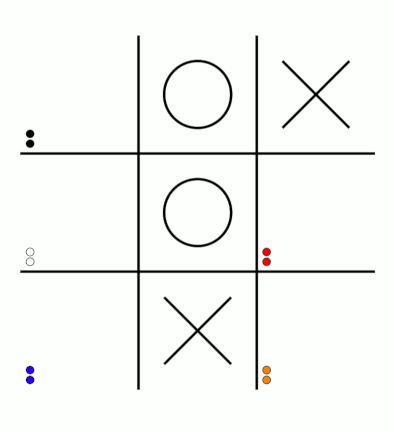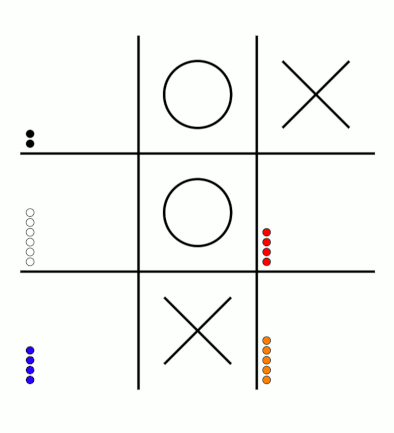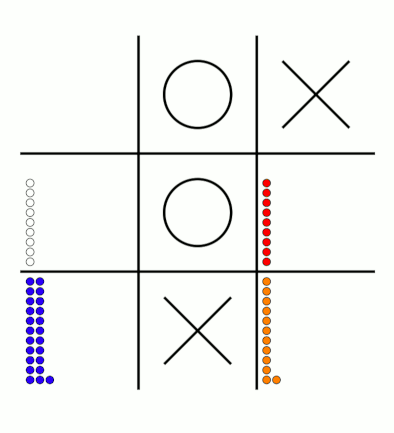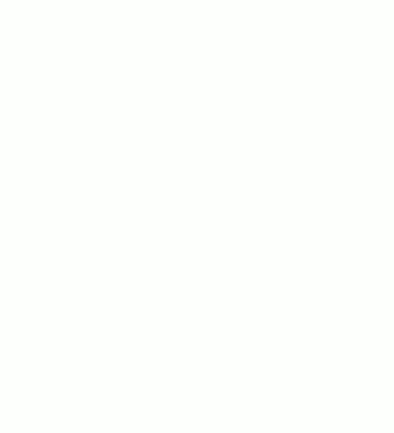
First up, here's a visualisation of the likelihood of MENACE choosing different moves as they play games. The thickness of each arrow represented the number of beads in the box corresponding to that move,
so thicker arrows represent more likely moves.
The likelihood that MENACE will play each move.
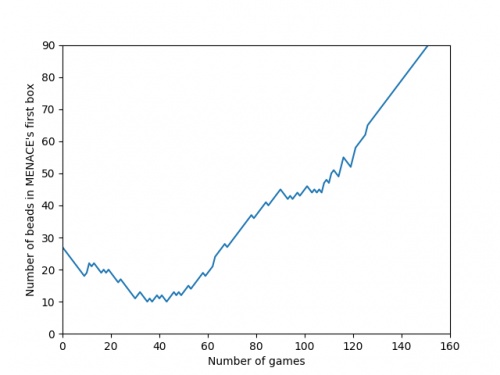
There's an awful lot of arrows in this diagram, so it's clearer if we just visualise a few boxes. This animation shows how the number of beads in the first box changes over time.
![](javascript:showlimage("MENACE_pos0.gif"))
The beads in the first box.
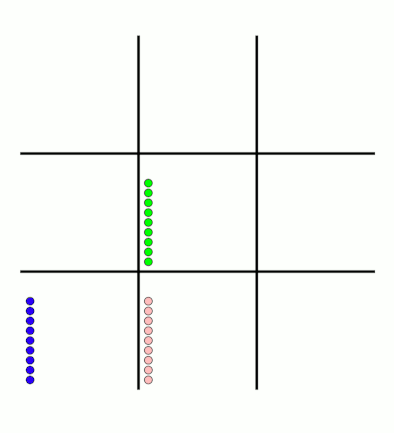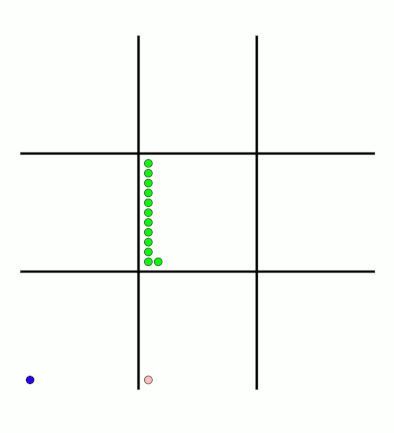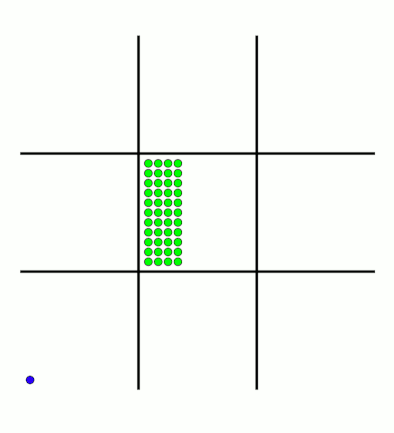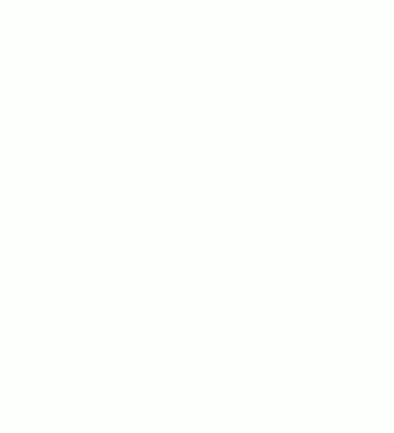
You can see that MENACE learnt that they should always play in the centre first, an ends up with a large number of green beads and almost none of the other colours. The following
animations show the number of beads changing in some other boxes.
![](javascript:showlimage("MENACE_pos4455.gif"))
MENACE learns that the top left is a good move.
![](javascript:showlimage("MENACE_pos13203.gif"))
MENACE learns that the middle right is a good move.
![](javascript:showlimage("MENACE_pos15396.gif"))
MENACE is very likely to draw from this position so learns that almost all the possible moves are good moves.
The numbers in these change less often, as they are not used in every game: they are only used when the game reached the positions shown on the boxes.
We can visualise MENACE's learning progress by plotting how the number of beads in the first box changes over time.
![](javascript:showlimage("MENACE_progress.png"))
The number of beads in MENACE's first box.
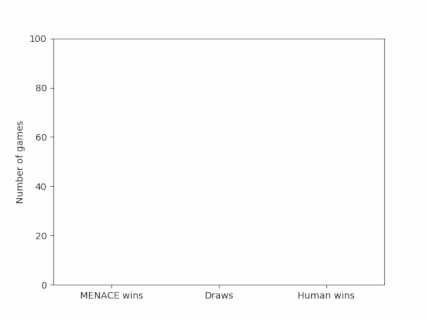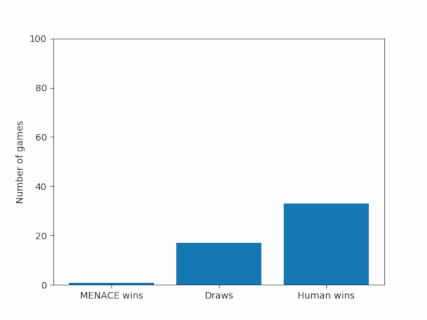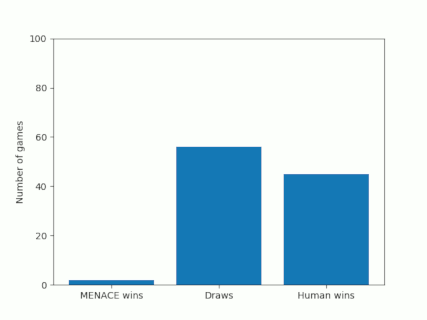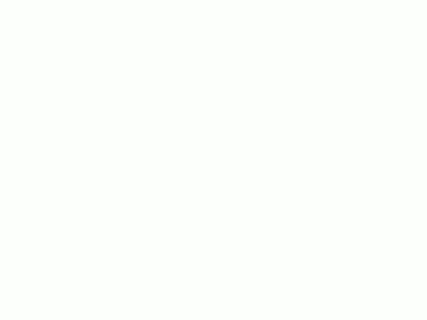
Alternatively, we could plot how the number of wins, loses and draws changes over time or view this as an animated bar chart.
![](javascript:showlimage("MENACE_progress_wld.png"))
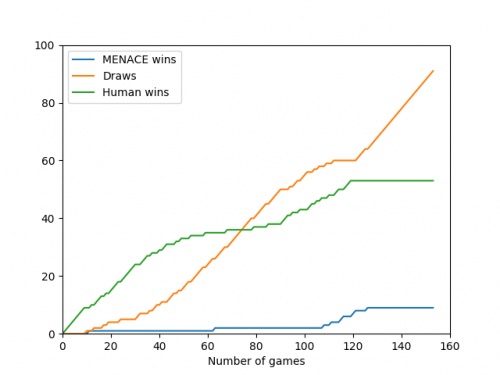
The number of games MENACE wins, loses and draws.
![](javascript:showlimage("MENACE_progress_wldbar.gif"))
The number of games MENACE has won, lost and drawn.
If you have any ideas for other interesting ways to present this data, let me know in the comments below.
×1 (Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@(anonymous): Have you been refreshing the page? Every time you refresh it resets MENACE to before it has learnt anything.
It takes around 80 games for MENACE to learn against the perfect AI. So it could be you've not left it playing for long enough? (Try turning the speed up to watch MENACE get better.)
It takes around 80 games for MENACE to learn against the perfect AI. So it could be you've not left it playing for long enough? (Try turning the speed up to watch MENACE get better.)
Matthew
I have played around menace a bit and frankly it doesnt seem to be learning i occasionally play with it and it draws but againt the perfect ai you dont see as many draws, the perfect ai wins alot more
(anonymous)
@Colin: You can set MENACE playing against MENACE2 (MENACE that plays second) on the interactive MENACE. MENACE2's starting numbers of beads and incentives may need some tweaking to give it a chance though; I've been meaning to look into this in more detail at some point...
Matthew
Idle pondering (and something you may have covered elsewhere): what's the evolution as MENACE plays against itself? (Assuming MENACE can play both sides.)
Colin
Add a Comment
2018-04-29
Two years ago, I built a copy of MENACE (Machine Educable Noughts And Crosses Engine). Since then, it's been to many Royal Institution masterclasses, visted Manchester and met David Attenborough. When I'm not showing them off, the 304 matchboxes that make up my copy of MENACE live in this box:
![](javascript:showlimage("menace-box.jpg"))
This box isn't very big, which might lead you to wonder how big MENACE-style machines would be for other games.
Hexapawn (HER)
In A matchbox game learning-machine by Martin Gardner [1], the game of Hexapawn was introduced. Hexapawn is played on a 3×3 grid, and starts with three pawns facing three pawns.
![](javascript:showlimage("hexapawn-start.png"))
The pieces move like pawns: they may be either moved one square forwards into an empty square, or take another pawn diagonally (the pawns are not allowed to move forwards two spaces on their first move, as they can in chess).
You win if one of your pawns reaches the other end of the board. You lose if none of your pieces can move.
The game was invented by Martin Gardner as a good game for his readers to build a MENACE-like machine to play against, as there are only 19 positions that can face player two, so only 19 matchboxes are needed to make HER (Hexapawn Educable Robot). (HER plays as player two, as if player two plays well they can always win.)
Nine Men's Morris (MEME)
In Nine Men's Morris, two players first take turns to place pieces on the board, before taking turns to move pieces to adjacent spaces. If three pieces are placed in a row, a player may remove one of the opponent's pieces. It's a bit like Noughts and Crosses, but with a bit more chance of it not ending in a draw.
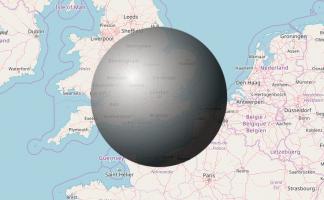
In Solving Nine Men's Morris by Ralph Gasser [2], the number of possible game states in Nine Men's Morris is given as approximately \(10^{10}\). To build MEME (Machine Educable Morris Engine), you would need this many matchboxes. These boxes would form a sphere with radius 41m: that's approximately the length of two tennis courts.
![](javascript:showlimage("menace-morris-sphere.png"))
MEME: Machine Educable Morris Engine
As a nice bonus, if you build MEME, you'll also smash the world record for the largest matchbox collection.
Connect 4 (COFFIN)
In Symbolic classification of general two-player games by Stefan Edelkamp and Peter Kissmann [3], the number of possible game states in Connect 4 is given as 4,531,985,219,092. The boxes used to make COFFIN (COnnect Four Fighting INstrument) would make a sphere with radius 302m: approximately the height of the Eiffel Tower.
![](javascript:showlimage("menace-connect4-sphere.png"))
COFFIN: COnnect Four Fighting INstrument
Draughts/Checkers (DOCILE)
In Solving the game of Checkers by Jonathan Schaeffer and Robert Lake [4], the number of possible game states in Draughts is given as approximately \(5\times10^{20}\). The boxes needed to build DOCILE (Draughts Or Checkers Intelligent Learning Engine) would make a sphere with radius 151km.
![](javascript:showlimage("menace-draughts-map.jpg"))
DOCILE: Draughts Or Checkers Intelligent Learning Engine
If the centre of DOCILE was in London, some of the boxes would be in Sheffield.
Chess (CLAWS)
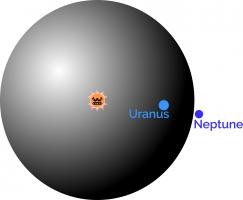
The number of possible board positions in chess is estimated to be around \(10^{43}\). The matchboxes needed to make up CLAWS (Chess Learning And Winning System) would fill a sphere with radius \(4\times10^{12}\)m.
![](javascript:showlimage("menace-chess-sphere.png"))
CLAWS: Chess Learning And Winning System
If the Sun was at the centre of CLAWS, you might have to travel past Uranus on your search for the right box.
Go (MEGA)
The number of possible positions in Go is estimated to be somewhere near \(10^{170}\). To build MEGA (Machine Educable Go Appliance), you're going to need enough matchboxes to make a sphere with radius \(8\times10^{54}\)m.
![](javascript:showlimage("menace-go-sphere.png"))
MEGA: Machine Educable Go Appliance
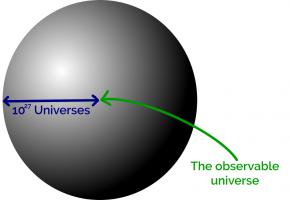
The observable universe takes up a tiny space at the centre of this sphere. In fact you could fit around \(10^{27}\) copies of the universe side by side along the radius of this sphere.
It's going to take you a long time to look through all those matchboxes to find the right one...
References
[3] Symbolic classification of general two-player games by Stefan Edelkamp and Peter Kissmann. in Advances in Artificial Intelligence (edited by A.R. Dengel, K. Berns, T.M. Breuel, F. Bomarius, T.R. Roth-Berghofer), 2008. [link]
[4] Solving the game of Checkers by Jonathan Schaeffer and Robert Lake. Games of No Chance 29, 1996. [link]
×1 ×1 ×2 (Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Kind of like the "Blue Brain Project". They got a worm and fruitfly brain on the computer, I wanted to download the fruitfly brain for 2GB USB stick but it was over 12 TB. They uploaded half a mouse brain on their project so far.
Willem
Would Love to play with Coffin/Coffin2. Do you have the code on git or a JS/web version?... been kind of thinking of coding a version that only makes the match boxes as it needs them (to save on memory) but I heard you already have a version with optimizations (and my coding skill is rough at best)
John
Are you aware of any actual implementations of anything in matchboxes, games or otherwise?
Jam
Of course, to make CLAWS, you will have to leave a large gap in the centre of the matchbox sphere, to avoid the very real danger of fire. Furthermore, some redundancy is needed, to replace the boxes which will be damaged by the myriad hard objects which are whizzing around the solar system. For this latter reason alone, I propose that the machine would be impractical to make! ;-D×1 ×1 ×1
g0mrb
×1 ×1 ×1 Add a Comment