Blog
Braiding, pt. 2: Two results and a conjecture
2016-06-29
In this blog post, I will present two conditions that cause a braid to
fail, with reasons why. You can read more about the method of braiding we
are talking about here, in part one.
In this post, we will consider the (\(a\),\(b\)) braid with \(a\) slits, taking the \(b\)th thread each time.
Some strands are never moved
If some of the strads are never moved in the braiding process, then the
braid will fail. To find out when this happens, I will draw lines to show the
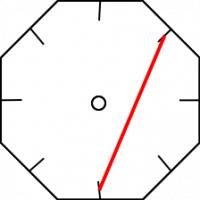
moves that are made. For the (8,3) braid, the first move is:
![](javascript:showlimage("brai-second1.png"))
Then the second move is:
![](javascript:showlimage("brai-second2.png"))
And so on until we get:
![](javascript:showlimage("brai-second3.png"))
For the (8,3) braid, every strand is moved at some point in the cycle.
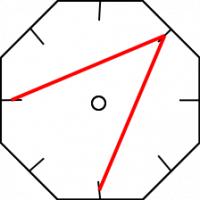
For the (6,2) braid, however, we get the following diagram:
![](javascript:showlimage("brai-third6.png"))
Now some strands are not moved and the braid will fail.
To find out when all the slits are visited, I first label the slots:
the slot which starts empty is 0, then I continue numbering anti-clockwise.
This numbering puts all the multiples of \(a\) at the bottom slot.
Now let's look at which slots we visit. We start at 0, then visit \(b\), then \(2b\), then \(3b\) and so on. We visit
all the multiples of \(b\).
Therefore we will reach the bottom slot again and finish our loop when we reach a common multiple of
\(a\) and \(b\). The first time this happens will be at the lowest common multiple, or \(\text{lcm}(a,b)\).
On the way to this slot, I visited one slot for every \(a\) we passed, so the number of slots I have visited is:
$$\frac{\text{lcm}(a,b)}{a}$$
I will visit every slot if:
$$\frac{\text{lcm}(a,b)}{a}=b$$
Or, in other words, if \(\text{lcm}(a,b)=ab\). This is true when, \(a\) and
\(b\) have no common factors, or are coprime: often written \(\text{hcf}(a,b)=1\).
Therefore, if \(a\) and \(b\) are not coprime, then the braid sill fail.
The braid results in twists
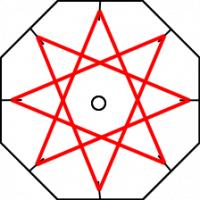
Some braids, for example (13,3), result in a groups of twisted strands rather than a whole braid.
![](javascript:showlimage("braiding/13-3.jpg"))
To see when this happens, imagine the (\(a\),\(b\)) braid just after a thread has been moved. Call the currently
empty slit 0. The threads at positions \(a-1\), \(a-2\), ..., \(a-b+1\) have just been jumped over. If, from these threads,
the thread at \(a-1\) is moved before the others, then this group of threads will form into a twist.
This will happen when \(b\) is a factor of \(a-1\), as this leads to \(a-1\) being reached before slit 0 is passed again.
Therefore is \(b\) is a factor of \(a-1\), the braid will not work.
A conjecture
In this post, I have shown that if \(a\) and \(b\) are not coprime or if \(b\) is a factor of \(a-1\), then the
braid will fail. From the examples I have tried (I'm compiling them here), it seems that
all other braids will work. It seems difficult, however, to explain why all other braids work. I'd love to hear your ideas
on how this could be shown.
What's next?
A have a few leads to follow up on, which may lead to a proof or counterexample.
Vicky
Neale has found instructions for making
Kumihimo braids. They
are created in a very similar way to my cardboard braids, so looking into
the patterns you can make with them may be helpful.
@mathforge
has found a mathoverflow
page where quotients of the braid group are discussed.
I know from past discussions that the braiding group is not exactly what I'm
looking for—for example, the multiple twists is considered a member of
the braiding group. However, finding the correct way to adapt the group may solve
the problem. Looks like I may have to polish up on my group theory...
Until a proof of or counterexample to the conjecture turns up, we seem to be at the end of the braiding puzzle.
But do not fret, there is a related problem that we can now spend some time on.
In the braids we've done so far, we have taken the same jump every time. But more complicated rules could be used:
for example, we could alternate between taking the third thread and the second thread. I'm yet to find a rule with different jumps
that works, so let me know if you find one before me!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment