Blog
2022-11-25
This year, the front page of mscroggs.co.uk will once again feature an Advent calendar, just like
in each of the last seven years.
Behind each door, there will be a puzzle with a three digit solution. The solution to each day's puzzle forms part of a logic puzzle:
It's nearly Christmas and something terrible has happened: an evil Christmas-hater has set three drones loose above Santa's stables. As long as the drones are flying around, Santa is unable to
take off to deliver presents to children all over the world.
You need to help Santa by destroying the drones so that he can deliver presents before Christmas is ruined for everyone.
Each of the three drones was programmed with four integers between 1 and 20 (inclusive): the first two of these are the drone's starting position; the last two give the drone's daily speed.
The drones have divided the sky above Santa's stables into a 20 by 20 grid. On 1 December, the drones will be at their starting position.
Each day, every drone will add the first number in their daily speed to their horizontal position, and the second
number to their vertical position. If the drone's position in either direction becomes greater than 20, the drone will subtract 20 from their position in that direction.
Midnight in Santa's special Advent timezone is at 5am GMT, and so the day will change and the drones will all move at 5am GMT.
For example, if a drone's starting position was (1, 12) and its movement was (5, 7), then:
- on day 1, it would be at (1, 12);
- on day 2, it would be at (6, 19);
- on day 3, it would be at (11, 6);
- on day 4, it would be at (16, 13);
- on day 5, it would be at (1, 20);
- on day 6, it would be at (6, 7);
- and so on.
You need to calculate each drone's starting position and daily speed, then work out where the drone currently is so you can shoot it down.
Behind each day (except Christmas Day), there is a puzzle with a three-digit answer. Each of these answers forms part of a piece of information about the locations of the drones.
You must use these clues to work out each drone's starting position and daily speed, then work out where the drone currently is so you can shoot it down.
You can use this page to fire up to 5 missiles into the sky each day.
Ten randomly selected people who solve all the puzzles, destroy all three drones, and fill in the entry form behind the door on the 25th will win prizes!
The prizes will include an mscroggs.co.uk Advent 2022 T-shirt. If you'd like one of the T-shirts from a previous Advent, they are available to order at merch.mscroggs.co.uk.
The winners will be randomly chosen from all those who submit the entry form before the end of 2022. Each day's puzzle (and the entry form on Christmas Day) will be available from 5:00am GMT. But as the winners will be selected randomly,
there's no need to get up at 5am on Christmas Day to enter!
As you solve the puzzles, your answers will be stored. To share your stored answers between multiple devices, enter your email address below the calendar and you will be emailed a magic link to visit on your other devices.
To win a prize, you must submit your entry before the end of 2022. Only one entry will be accepted per person. If you have any questions, ask them in the comments below,
on Twitter,
or on Mastodon.
So once December is here, get solving! Good luck and have a very merry Christmas!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
⭐ top comment (2022-12-25) ⭐
My dad and I did several of these puzzles together. I am 8 years old, and I figured many of them out. Thank you!Xena
It's becoming a Christmas tradition to do your advent calendar with my partner. Loved being able to narrow down our guesses each day to pinpoint the drone this time around. Thanks for running this!
Liz
Another year of great puzzles, Matt! I really appreciate it and look forward to working these every year.
Dan Whitman
Really enjoyable this year. I "give" this advent calendar to my Year 12 and 13 Further Maths classes every year, and this has engaged more of them than in previous years. They particularly liked the shooting down of drones and the opportunity for intelligent "guess work" or in the case of some writing a computer programme which would calculate the probability distribution for each drone's position based on current information. Thank you
TAS
Thanks so much for making this, Matthew! It was a joy to solve, I found myself looking forward to every morning.
Tyler St Clare
Add a Comment
2022-01-08
Welcome to 2022 everyone! Now that the Advent calendar has disappeared, it's time to reveal the answers and annouce the winners.
But first, some good news: with your help, a successful test flight was made and Christmas was saved!
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar, reveal the solution and a couple of other interesting bits and pieces.
Highlights
My first highlight is the puzzle from 2 December. I like this puzzle, as it's very difficult (maybe impossible) to work out by
brute force (as \(n\) is a huge number), and the solution method I used was satisfying.
2 December
The number \(7n\) has 37 factors (including 1 and the number itself). How many factors does \(8n\) have?
There was a typo in this puzzle. It originally read "38 factors" when it was meant to say "37 factors".
My next hightlight is the puzzle from 5 December. It's difficult to find many triangles with
perimeter 50 and an integer area, but there's a neat way to solve this without needing to find any.
5 December
How many different isosceles triangles are there whose perimeter is 50 units, and whose area is an integer number of square-units?
(Two triangles that are rotations, reflections and translations of each other are counted as the same triangle. Triangles with an area of 0 should not be counted.)
My next highlight is the puzzle from 14 December. This is closely related to the puzzle
from 12 December but this time movements to the left are allowed.
I enjoyed a nice "aha!" moment when designing this puzzle.
14 December
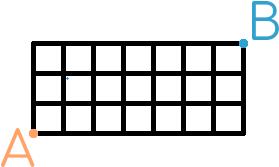
You start at the point marked A in the picture below. You want to get to the point marked B. You may travel to the right, upwards, or to the left along the black lines, but you cannot pass along the same line segment more than once.
Today's number is the total number of possible routes to get from A to B.
My final highlight is the puzzle from 16 December. If you enjoyed this one, you'll
probably also enjoy the crossnumber I wrote for Chalkdust issue 13.
16 December
Each clue in this crossnumber is formed of two parts connected by a logical connective:
and means that both parts are true;
nand means that at most one part is true;
or means that at least one part is true;
nor means that neither part is true;
xor means that exactly one part is true;
xnor means that either both parts are false or both parts are true.
No number starts with 0.
|
1A is a palindrome xnor 1D is a palindrome.
1A is greater than 350 nor 1D is less than 150.
3D is odd nand 4A and 2D are equal.
3D is prime xor 5A is odd.
4A is a cube and 2D is a cube.
The sum of the digits of 3D is 2 or the sum of the digits of 5A is 5.
Today's number is 1D.
|
Hardest and easiest puzzles
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
You can see that the most difficult puzzles were those on
5 and
14 December;
and the easiest puzzles were on
6,
8, and
9 December.
An Easter egg
The numbers on the doors of the Advent calendar formed a magic square: the numbers in each row, each
column, and on the two major diagonals all add up to the same total.
This was spotted by
both Colin Beveridge (@icecolbeveridge)
and Alex on 15 December.
The winners
And finally (and maybe most importantly), on to the winners: 150 people solved all the puzzles and made a successful test flight. That's down on last year but up on two years ago:
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
| Year | ||||||
From the correct answers, the following 10 winners were selected:
- Shivanshi
- LycanFayn
- Colin Beveridge
- Katharine Velleman
- Gregory Wheeler
- Alex Bolton
- Don Anderson
- Dan Colestock
- Pamela Docherty
- Annabel
Congratulations! Your prizes will be on their way shortly.
The prizes this year include 2021 Advent calendar T-shirts. If you didn't win one, but would like one of these, I've made them available to buy at merch.mscroggs.co.uk alongside the T-shirts from previous years.
Additionally, well done to
Aaron Stiff, Alan Buck, Alanis, Alek2ander, Alex, Alex Davis, Andrew Brady, Andrew Roy, Andrew Turner, Austin,
B Moreland, Becky Russell, Ben Baker, Ben Boxall, Ben Jones, Ben Reiniger, Ben Tozer, Berl Steiner, Brennan Dolson, Brian Carnes, Brian Wellington,
Carl Westerlund, Carmen, Cathy Hooper, Chris Hellings, Christopher Adams, Christy Hales, Connie, Corbin Groothuis, CreativeCrocheter,
Dan DiMillo, Dan Whitman, Daniel Chiverton, Daniel Low, Dave Budd, David Ault, David Berardo, David Fox, David Kendel, David Mitchell, David P, David and Ivy Walbert, Deborah Tayler, Dylan Madisetti,
Elijah Kuhn, Emily Troyer, Eric, Eric Kolbusz, Erik Eklund,
Frank Kasell, Franklin Ta, Fred Verheul,
Gabriella Pinter, Gary M. Gerken, Gert-Jan de Vries, Gregory Loges, Gwendolenn,
Hannah , Harry Allen, Heerpal Sahota, Helen, Helen Bradley, Håkon Balteskard,
Iris,
Jacob Y, James Chapman, Jarvis, Jay Miller, Jean-Noël Monette, Jean-Sébastien Turcotte, Joe Gage, John Alasdair Warwicker, Jon Palin, Jonathan Chaffer, Jonathan Winfield, Jorge del Castillo, Joseph Wagner,
Kai, Karen Climis, Kim Brooks, Kristen Koenigs,
Lauren Woolsey, Lemminkäinen, Lewis Dyer, Liz Madisetti, Louis, Luke S,
Maggie Orr, Magnus Eklund, Marco van der Park, Maria, Mark Stambaugh, Martin Harris, Martin Holtham, Matt Askins, Matthew, Matthew Schulz, Mels, Michael DeLyser, Mihai Zsisku, Mike Hands, Millie,
NIck C, Nadine Chaurand, Naomi Bowler, Nick Keith, Niji, Nikos I., Noah Overcash,
Oscar, Friend of Rudolph,
patrick fussell,
Ray Arndorfer, Rea, Reuben Cheung, Riccardo Lani, Rick Simineo, Robert Brady, Roger Lipsett, Rosie Paterson, Russ Collins, Ruth, Ryan W,
Scott, Sean Carmody, Sean Henderson, Seth Cohen, SherlockSage, Simon Schneider,
Tamara Brenner, Tarim, Tom Fryers, Tony Mann, tripleboleo, Tristan S,
UsrBinPRL,
Valentin VĂLCIU, Vinayak,
Yasha, Yuliya Nesterova, and Yurie Ito,
who all also completed the Advent calendar but were too unlucky to win prizes this time or chose to not enter the prize draw.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
I feel compelled to admit that something over a hundred of the checks on day 14 were me after I gave up all hope of figuring out the elegant solution and just started counting up from what I had come up with as a lower limit. I really, really wanted a go at the logic puzzle.
At least my failed attempt to figure that one made me realize that I needed to change my answer to day 12.
At least my failed attempt to figure that one made me realize that I needed to change my answer to day 12.
Kim
Damn, missed out again! But had a lot of fun (again). I'd guess the reason for there being fewer successful entries this year was the final puzzle being much harder than previous years, rather than a drop in participation. I got worried I still hadn't solved it on the 30th and had to get my whole family involved!
Louis
Thanks for the advert calendar this year.
By the way, in the "Hardest and easiest puzzles" section, 4 out of the 5 links to the puzzles are to the 2020 puzzles instead of the 2021 puzzles
By the way, in the "Hardest and easiest puzzles" section, 4 out of the 5 links to the puzzles are to the 2020 puzzles instead of the 2021 puzzles
Alex
My son and I really enjoyed solving the puzzles each day. As a mom whose son is thousands of miles away, it was a great way to connect each day of Advent. This is our second year and I will definitely order a tee shirt. Keep up the great work!
Liz
Add a Comment
2021-12-04
In November, I spent some time designing this year's Chalkdust puzzle Christmas card.
The card looks boring at first glance, but contains 14 puzzles. By writing the answers to the puzzles in the triangles on the front of the card, then colouring triangles containing 1s, 2s, 5s or 6s in the right colour, you will reveal a Christmas themed picture.
If you want to try the card yourself, you can download this printable A4 pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will automatically be written in the triangles, and the triangles will be coloured...
The puzzles | ||
| 1. | What is the sum of all the odd integers between 0 and 30? | Answer |
| 2. | What is the sum of all the odd integers between 0 and 5668? | Answer |
| 3. | What is the smallest integer with a digital sum of 28 and a digital product of 10000? | Answer |
| 4. | What is the smallest integer with a digital sum of 41 and a digital product of 432000? | Answer |
| 5. | What is the area of the largest area dodecagon that will fit inside a circle with area \(111185\pi\)? | Answer |
| 6. | What is the area of the largest area heptagon that will fit inside a semicircle with area \(115185\pi\)? | Answer |
| 7. | How many terms are there in the (simplified) expansion of \((x+y+z)^{2}\)? | Answer |
| 8. | How many terms are there in the (simplified) expansion of \((x+y+z)^{41172}\)? | Answer |
| 9. | What is the largest integer that cannot be written as \(4a+5b\) for non-negative integers \(a\) and \(b\)? | Answer |
| 10. | What is the largest integer that cannot be written as \(83409a+66608b\) for non-negative integers \(a\) and \(b\)? | Answer |
| 11. | How many positive integers are there below 100 whose digits are all non-zero and different? | Answer |
| 12. | How many positive integers are there whose digits are all non-zero and different? | Answer |
| 13. | What is the only integer for which taking the geometric mean of all its factors (including 1 and the number itself) gives 2? | Answer |
| 14. | What is the only integer for which taking the geometric mean of all its factors (including 1 and the number itself) gives 25? | Answer |
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@HJ: the smallest one does have 6, and Q4 is correct too. I bought the cards and had good fun solving it myself. I’m glad to find this here though to check my answers as when I did the shading it looked like the picture wasn’t quite right. Thanks for the cards Matthew, I look forward to next year’s - no pressure!
Alec
The only one I'm stuck on is #6. I thought I was doing it right but I'm getting a non-integer answer. I'm assuming the heptagon in question is aligned so one of its sides sits on the diameter of the semicircle, and the opposite vertex sits on the curved edge of the semicircle. Is this wrong?
Seth C
The version of the card on this page doesn't check if your answers are correct, so it will colour in any number you enter as long as it has the right number of digits.
Matthew
Wonky solution for #9? On a blank start page, answering "16" gives you red and white puzzle completions, yet we _know_ that 16 is an incorrect answer. Strange?
Attika
Add a Comment
2021-11-25
This year, the front page of mscroggs.co.uk will once again feature an Advent calendar, just like
in each of the last six years.
Behind each door, there will be a puzzle with a three digit solution. The solution to each day's puzzle forms part of a logic puzzle:
It's nearly Christmas and something terrible has happened: a saboteur has infiltrated the stables where Santa's reindeer are kept, and has caused all three of Santa's test flights to be unsuccessful.
You need to help Santa have a successful test flight so that he can deliver presents before Christmas is ruined for everyone.
In order to have enough magical power to fly with the sleigh, all nine of Santa's reindeer must be fed their favourite food. The saboteur gave one or more reindeer the wrong food before each of
the three test flights, causing the reindeer to be unable to take off.
Behind each day (except Christmas Day), there is a puzzle with a three-digit answer. Each of these answers forms part of a piece of information about the reindeer's favourite foods and what
the reindeer were fed before the three test flights. In each clue, "before test flight n" means "immediately before test flight n". Before each test flight, each reindeer was fed exactly one
food, and two or more reindeer may have been fed the same food. Two or more reindeer may have the same favourite food. You must use these clues to work out what each reindeer's favourite food is, then complete a test flight by feeding each reindeer the correct food.
You can use this page to attempt up to three test flights per day. An attempted test flight will be successful if and only if all nine reindeer are given their favourite food just before the flight.
Ten randomly selected people who solve all the puzzles, complete a successful test flight, and fill in the entry form behind the door on the 25th will win prizes!
The prizes will include an mscroggs.co.uk Advent 2021 T-shirt. If you'd like one of the T-shirts from a previous Advent, they are available to order at merch.mscroggs.co.uk.
The winners will be randomly chosen from all those who submit the entry form before the end of 2021. Each day's puzzle (and the entry form on Christmas Day) will be available from 5:00am GMT. But as the winners will be selected randomly,
there's no need to get up at 5am on Christmas Day to enter!
As you solve the puzzles, your answers will be stored. To share your stored answers between multiple devices, enter your email address below the calendar and you will be emailed a magic link to visit on your other devices.
To win a prize, you must submit your entry before the end of 2021. Only one entry will be accepted per person. If you have any questions, ask them in the comments below or on Twitter.
So once December is here, get solving! Good luck and have a very merry Christmas!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Thanks Matthew. Really nice to have this daily dose of brain teasing again
Gert-Jan
This was a lot of fun - thank you so much for the time and effort that went into this.
Each puzzle was tricky enough to require some thought, but not so tricky as to be discouraging.
Looking forward to next year already!
Each puzzle was tricky enough to require some thought, but not so tricky as to be discouraging.
Looking forward to next year already!
Si E
Thanks, Matthew for all of your hard work to create the Advent Calendar. It was so much fun to work together with my son, even though we live thousands of miles apart. He is a coder and I am definitely old-school math.
Liz
I have really enjoyed these puzzles over the last 26 days. I particularly liked the variety of puzzles, some leading me to graphing software, others to my amateur coding, and many just to a piece of paper and a pencil. Some ideas for the classroom too!
Ben
@(anonymous): Yes, you should have enough info to work all that out. I recommend using a spreadsheet to keep track of all the feedings.
Matthew
Really struggling with the final logic puzzle this year...is it possible to work out what each reindeer was fed before each test flight as well as their favourite foods? The information seems so little!
(anonymous)
Add a Comment
2021-01-03
It's 2021, and the Advent calendar has disappeared, so it's time to reveal the answers and annouce the winners.
But first, some good news: with your help, Santa received all his letters and Christmas was saved!
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar, reveal the solution and a couple of other interesting bits and pieces.
Highlights
My first highlight is this puzzle from 5 December, that I think doesn't seem obvious that there's even a unique answer until you spot some nice properties of
dice.
5 December
Carol rolled a large handful of six-sided dice. The total of all the numbers Carol got was 521. After some calculating, Carol worked out that the probability that of her total being 521
was the same as the probability that her total being 200. How many dice did Carol roll?
My next highlight is the puzzle from 15 December. I had a lot of fun trying to write this one. At the end, I tell you that T represents 4: this puzzle still has a unique answer without this,
but it was too hard to get started.
15 December
When talking to someone about this Advent calendar, you told them that the combination of XMAS and MATHS is GREAT.
They were American, so asked you if the combination of XMAS and MATH is great; you said SURE. You asked them their name; they said SAM.
Each of the letters E, X, M, A, T, H, S, R, U, and G stands for a different digit 0 to 9. The following sums are correct:
|
| ||||||||||||||||||||||||||||||||||
Today's number is SAM. To help you get started, the letter T represents 4.
My next highlight is the puzzle from 16 December. I had a lot of fun writing this one too. At least a few people seem to have enjoyed solving it,
as indicated by this comment.
16 December
Solve the crossnumber to find today's number. No number starts with 0.
|
| |||||||||||||||||||||||||||||||||
My final highlight is the puzzle from 21 December. My method for solving this one was quite complicated. Let me know in the comments or on Twitter if you have a better way of solving it.
21 December
There are 3 ways to order the numbers 1 to 3 so that no number immediately follows the number one less that itself:
- 3, 2, 1
- 1, 3, 2
- 2, 1, 3
Today's number is the number of ways to order the numbers 1 to 6 so that no number immediately follows the number one less that itself.
Hardest and easiest puzzles
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
You can see that the most difficult puzzles were those on
6,
14,
19,
21, and
24 December;
and the easiest puzzles were on
3,
9,
10,
16, and
17 December.
The solutions
The solutions to all the individual puzzles can be found here. If you want to read some alternative solutions to the puzzles, you can find Alira's solutions here, including a very nice explanation of how the final clues fit together to find the directions to Santa's house.
Using the daily clues, it was possible to work out that Santa's house could be found by following the directions 3,7,1,1,4,3,3,4,9,3,3,9 on this map.
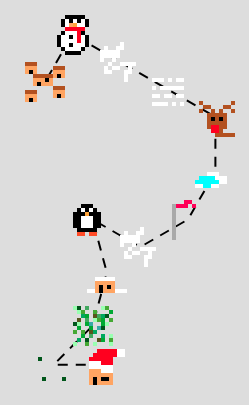
Directions to Santa's house.
Due to the way the Advent compass worked, there are actually a few different ways to get to Santa's house. For example, 7,5,7,1,1,4,3,3,4,9,3,3 also gets you there:
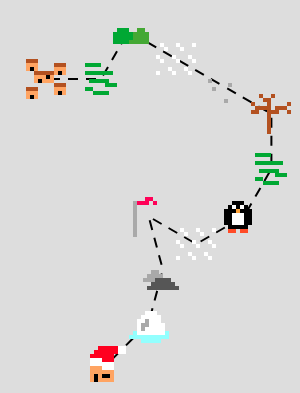
Alternative directions to Santa's house.
I'll leave you to work out how many different ways there are to get there...
Here's the full collection of tiles that you could find by walking around the map:
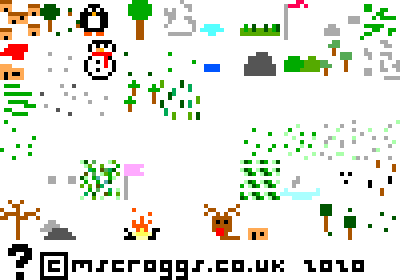
The map tiles.
The winners
And finally (and maybe most importantly), on to the winners: 223 people found Santa's house entered the competition. This is quite a lot more than in previous years:
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
| Year | |||||
From the correct answers, the following 10 winners were selected:
| 1 | Mars He |
| 2 | Ben Baker |
| 3 | Amelia Taylor |
| 4 | Alex Ayres |
| 5 | Hannah Charman |
| 6 | Diane Keimel |
| 7 | Alex Burlton |
| 8 | Rob March |
| 9 | Mahmood Hikmet |
| 10 | Guillermo Heras Prieto |
Congratulations! Your prizes will be on their way shortly.
The prizes this year include 2020 Advent calendar T-shirts. If you didn't win one, but would like one of these, I've made them available to buy at merch.mscroggs.co.uk alongside the T-shirts from previous years.
Additionally, well done to
4nder, Ashley Frazer Jarvis, Aaron Stiff, Alan Buck, Alejandro Villarreal, Alex Bolton, Alex Davis, Alex Klapheke, Alexander Rakitin, Anders Kaseorg, Andrew, Andrew P Turner, Andy Ennaco, Annabel, Anthony Della Pella, Artie Smith, Athena, Austin, Austin Shapiro, Beau Ferguson, Becky Russell, Ben Buchwald, Ben Jones, Ben Reiniger, Benjamin Tozer, Bennet, Beth Jensen, Blake, Brennan Dolson, Brian Carnes, Brian Wellington, Burak Kadron, Caleb Likely, Callum Hobbis, Carl Westerlund, Carmen Günther, Cath Simpson, Cathy Hooper, Chris Hellings, Christy Hales, Colin, Colin Brockley, Connie, Corbin Groothuis, Cory Peters, Cosmo Viola, Dan Colestock, Dan DiMillo, Dan McIntyre, Dan Whitman, Dana Sussman, Daniel De la Paz, David, David Ault, David Berardo, David Fox, David Kendel, David Mitchell, David Parmenter, David and Ivy Walbert, Dean Thomas, Deborah Tayler, Don Anderson, Donagh Collins, Elizabeth Blackwell, Emilie Heidenreich, Emily Troyer, Eric Kolbusz, Eric Skoglund, Erik Eklund, Eva, Evan Louis Robinson, Fionn Woodcock, Frances Haigh, Frank Kasell, Franklin Ta, Fred Verheul, Georges, Gabriella Pinter, Gert-Jan de Vries, Graham Greve, Gregory Loges, Gwendal Collet, Harry Allen, Heerpal Sahota, Helen, Helen Matthews, Herschel Pecker, Håkon Balteskard, Ivan Arribas, Jacob Young, James Demers, James Laver, Jan, Jason Demers, Jason Kass, Jean-Sébastien Turcotte, Jeff Rubin, Jefff Michael, Jen Huang, Jessica Marsh, Jim Rogers, Joe Gage, Johan Asplund, John Alasdair Warwicker, Jon Foster, Jon Lipscombe, Jon Palin, Jonathan Chaffer, Jonathan Forsythe, Jonathan Winfield, Jordan Susskind, Jorge del Castillo, Kai Lam, Karen Climis, Keith Pound, Ken Cheung, Killeen, Kristen Koenigs, Kristin Gramza, Kurt Engleman, Laura Midgley, Lauren Woolsey, Lewis Dyer, Linus Banghart-Linn, Liz Madisetti, Louis de Mendonca, Magnus Eklund, Mark Stambaugh, Martijn O., Martin Harris, Martin Holtham, Martine Nome, Matt Askins, Matt Hutton, Matthew Reynier, Matthew Riggle, Matthew Schulz, Matthew Scroggs, Matthias Planitzer, Maxime Rivet, Maximilian Pfister, Michael DeLyser, Michael Prescott, Mihai Zsisku, Mike Hands, Moritz Stocker, Nadine Chaurand, Nathan Chun, Nick C, Nick Keith, Nick Mohr, Norvin Richards, Olov Wilander, Pamela Docherty, Pau Batlle, Paul Livesey, Pranshu Gaba, Ray Arndorfer, Rea, Reuben Cheung, Riccardo Lani, Richard Pemberton, Rileigh Luczak, Road White, Roni, Rosie Paterson, Russ Collins, Ruth Franklin, Ryan Coomer, Ryan Seldon, Ryan Wise, Sam Dreilinger, Sam Hartburn, Sammie Buzzard, Sara Van Hoy, Sarah Brook, Saul Freedman, Scott, Sean, Sean Carmody, Sean Henderson, Sean McDonald, Sebastian, Selina Glauert, Seth Cohen, Shivanshi Adlakha, Simon Schneider, Sophie Maclean, Spencer B., Stephen Cappella, Stephen Dainty, Stephen Jasina, Steve Blay, Steve Paget, Steven Richardson, Susana Early, Tarim, Tim Holman-Wilkens, Tim Lewis, Todd Geldon, Tom Fryers, Tony Mann, Tristan Shephard, Valentin Valciu, Vinesh, Yasha, Yuliya Nesterova, Yurie Ito, and Zachary Polansky
who all also found Santa's house but were too unlucky to win prizes this time.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Dec 15th was my favorite. I kept making a logical error and had to restart, so it took me way to long, but I really enjoyed it.
The 16th was just cheeky, after I spent way to much time on the 15th it was nice to have something like that!
It's been 16+ years since I did any probability or combinations and permutations, so it was nice to brush off that part of my brain, not that I did any of them well, but it should serve me well when my kids start doing them and ask me for help.
The 16th was just cheeky, after I spent way to much time on the 15th it was nice to have something like that!
It's been 16+ years since I did any probability or combinations and permutations, so it was nice to brush off that part of my brain, not that I did any of them well, but it should serve me well when my kids start doing them and ask me for help.
Dave
You can solve the Dec 21 puzzle using the principle of inclusion/exclusion:
-There are 6! total ways of arranging 6 numbers.
-Now we have to exclude the ones that don't fit. How many ways have 2 following 1? You can think of 12 as a pair, so you're arranging 12/3/4/5/6 in any order, so there are 5! ways to do this. And there are (5 choose 1)=5 total pairs that might exist, so there are 5*5! ways that have either 12, 23, 34, 45, or 56.
-Of course, we've double counted some that have more than one pair. (This is where inclusion/exclusion comes in, we have to include them back in). So how many have, say, 12 and 45? Well now we're arranging 12/3/45/6, so there are 4! ways to do so. There are (5 choose 2)=10 different pairs, so the double counting was 10*4!.
-We continue this on, and inclusion/exclusion says we keep alternating adding and subtracting as we add more pairs, so the answer is:
6!
- (5 choose 1) * 5!
+ (5 choose 2) * 4!
- (5 choose 3) * 3!
+ (5 choose 4) * 2!
- (5 choose 5) * 1!
= 309
-There are 6! total ways of arranging 6 numbers.
-Now we have to exclude the ones that don't fit. How many ways have 2 following 1? You can think of 12 as a pair, so you're arranging 12/3/4/5/6 in any order, so there are 5! ways to do this. And there are (5 choose 1)=5 total pairs that might exist, so there are 5*5! ways that have either 12, 23, 34, 45, or 56.
-Of course, we've double counted some that have more than one pair. (This is where inclusion/exclusion comes in, we have to include them back in). So how many have, say, 12 and 45? Well now we're arranging 12/3/45/6, so there are 4! ways to do so. There are (5 choose 2)=10 different pairs, so the double counting was 10*4!.
-We continue this on, and inclusion/exclusion says we keep alternating adding and subtracting as we add more pairs, so the answer is:
6!
- (5 choose 1) * 5!
+ (5 choose 2) * 4!
- (5 choose 3) * 3!
+ (5 choose 4) * 2!
- (5 choose 5) * 1!
= 309
Todd
Add a Comment