Advent calendar 2015
24 December
Today's number is the largest possible remainder which can be obtained when dividing one of
the answers in this advent calendar by another answer smaller than it (not
including today's answer!).
23 December
This number is a prime number. If you treble it and add 16, the result is also prime. Repeating this will give 11 prime numbers in total (including the number itself).
22 December
What is the largest number which cannot be written as the sum of distinct squares?
21 December
This year, I posted instructions for making a dodecahedron and a stellated rhombicuboctahedron.
To get today's number, multiply the number of modules needed to make a dodecahedron by half the number of tube maps used to make a stellated rhombicuboctahedron.
20 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
| + | - | = 8 | |||
| - | - | - | |||
| + | ÷ | = 9 | |||
| + | ÷ | × | |||
| + | × | = 108 | |||
| = 6 | = 1 | = 18 |
The answer is the product of the digits in the red boxes.
19 December
1 = 1/2 + 1/4 + 1/8 + 1/16 + 1/16. This is the sum of 5 unit fractions (the numerators are 1).
In how many different ways can 1 be written as the sum of 5 unit fractions? (the same fractions in a different order are considered the same sum.)
18 December
Put the digits 1 to 9 (using each digit once) in the boxes so that the three digit numbers formed (reading left to right and top to bottom) have the desired properties written by their rows and columns.
| multiple of 9 | |||
| multiple of 3 | |||
| multiple of 5 | |||
| multiple of 6 | multiple of 4 | cube number |
Today's number is the multiple of 6 formed in the left hand column.
17 December
In March, I posted the puzzle One Hundred Factorial, which asked how many zeros 100! ends with.
What is the smallest number, n, such that n! ends with 50 zeros?
16 December
Today's number is four thirds of the average (mean) of the answers for 13th, 14th, 15th and 16th December.
15 December
If the numbers 1 to 7 are arranged 7,1,2,6,3,4,5 then each number is either larger than or a factor of the number before it.
How many ways can the numbers 1 to 7 be arranged to that each number is either larger than or a factor of the number before it?
14 December
What is the only palindromic three digit prime number which is also palindromic when written in binary?
13 December
Put the digits 1 to 9 (using each digit once) in the boxes so that the three digit numbers formed (reading left to right and top to bottom) have the desired properties written by their rows and columns.
The row marked sum is equal to the sum of the other two rows. The column marked sum is equal to the sum of the other two columns.
| odd | |||
| all digits even | |||
| sum | |||
| even | odd | sum |
Today's number is the largest three digit number in this grid.
12 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
| + | - | = -2 | |||
| - | - | - | |||
| + | ÷ | = 4 | |||
| + | ÷ | × | |||
| + | × | = 50 | |||
| = 4 | = -4 | = 10 |
The answer is the product of the digits in the red boxes.
11 December
This year, I was involved in starting Chalkdust Magazine. One of my roles for the magazine has been writing the £100 crossnumber puzzle.
What is the answer to 35 across in the first issue's crossnumber?
35A. The smallest number which is one more than triple its reverse. (3)
10 December
This number is divisible by 2. One more than this number is divisible by 3. Two more than this number is divisible by 5. Three more than this number is divisible by 7. Four more than this number is divisible by 11. Five more than this number is divisible by 13.
9 December
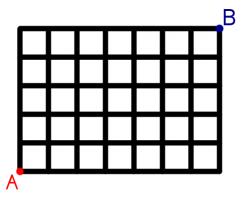
You start at A and are allowed to move either to the right or upwards.
How many different routes are there to get from A to B?
8 December
What is the largest number of factors which a number less than a million has?
7 December
In September, my puzzle appeared as Alex Bellos's Monday Puzzle. The puzzle asked what the highest rugby score was which can only be made with one combination of kicks, tries and converted tries.
What is the highest rugby score which can be made with 101 different combinations of kicks, tries and converted tries?
6 December
Put the digits 1 to 9 (using each digit once) in the boxes so that the three digit numbers formed (reading left to right and top to bottom) have the desired properties written by their rows and columns.
| multiple of 5 | |||
| multiple of 7 | |||
| cube number | |||
| multiple of 9 | multiple of 3 | multiple of 4 |
Today's number is the multiple of 5 formed in the first row.
5 December
How many different triangles are there with a perimeter of 100 and each side
having an integer length?
(different = not rotations or reflections)
4 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
| - | + | = -4 | |||
| + | + | + | |||
| - | ÷ | = -1 | |||
| - | ÷ | × | |||
| - | × | = -30 | |||
| = 0 | = 2 | = 54 |
The answer is the product of the digits in the red boxes.
3 December
In August, I wrote about MENACE, a machine learning robot built from matchboxes which plays noughts and crosses. How many matchboxes are needed to build MENACE?
2 December
In a week (Monday 12:01 to Monday 12:01 a week later), how many times will the minute hand of an analogue clock point in the same direction as the hour hand?
1 December
What is area of the largest area rectangle which will fit in a circle of radius 10?