Puzzles
7 December
What is the area of the largest triangle that fits inside a regular hexagon with area 952?
Show answer
Hide answer
The vertices of this triangle will be every other vertex of the hexagon: and other triangle can be made larger by moving one of its vertices closer to a vertex of the hexagon.
The area of this triangle is 476.
5 December
How many different isosceles triangles are there whose perimeter is 50 units, and whose area is an integer number of square-units?
(Two triangles that are rotations, reflections and translations of each other are counted as the same triangle. Triangles with an area of 0 should not be counted.)
Show answer
Hide answer
The largest possible isosceles triangles with a perimeter of 50 units is the equilateral triangle with sides of length 50/3. The area of this triangle is 120.28 square-units.
By continuously adjusting the width of the base of the isosceles triangle, triangles with every area between 0 and 120.28 can be created. The animation below shows this.
Triangles with areas of each integer from 1 to 120 can therefore be created. Each area can be made twice: once with a tall and thin triangle, and once with a short and wide triangle.
This means that there are 240 different triangles with a perimeter of 50 units and an integer area.
12 December
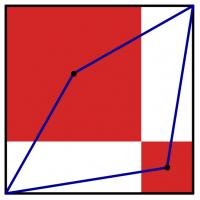
The diagram to the left shows a large black square. Inside this square, two red squares have been drawn.
(The sides of the red squares are parallel to the sides of the black square; each red square shares a vertex with the black square; and the two red squares share a vertex.)
A blue quadrilateral has then been drawn with vertices at two corners of the black square and the centres of the red squares.
The area of the blue quadrilateral is 167. What is the area of the black square?
Show answer
Hide answer
No matter the exact size of each square, the blue quadrilateral will always fill half the square, so the area of the square is 334.
2 December
Carol draws a square with area 62. She then draws the smallest possible circle that this square is contained inside.
Next, she draws the smallest possible square that her circle is contained inside. What is the area of her second square?
Show answer
Hide answer
By drawing an appropriate diagram, it can be seen that the small square has half the area of the large square.
Therefore the area of the large square is 124.
23 December
Today's number is the area of the largest area rectangle with perimeter 46 and whose sides are all integer length.
2 December
Today's number is the area of the largest dodecagon that it's possible to fit inside a circle with area \(\displaystyle\frac{172\pi}3\).
Squared circle
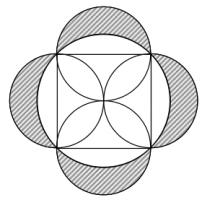
Each side of a square has a circle drawn on it as diameter. The square is also inscribed in a fifth circle as shown.
Find the ratio of the total area of the shaded crescents to the area
of the square.
Show answer
Hide answer
Let the radius of the small circles be \(r\). The are of half of one of these circles is \(\frac{1}{2}\pi r^2\).
The side of the square is \(2r\) and so the area of the square is \(4r^2\). Therefore the area of the whole shape is \((4+2\pi)r^2\).
By Pythagoras' Theorem, the radius of the large circle is \(r\sqrt{2}\). Therefore the area of the circle is \(2\pi r^2\). This means that the shaded area is \((4+2\pi)r^2 - 2\pi r^2\) or \(4r^2\).
This is the same as the area of the square, so the ratio is 1:1.
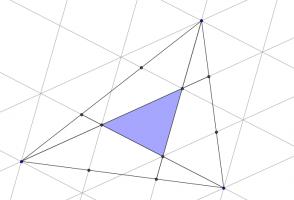
Two triangles
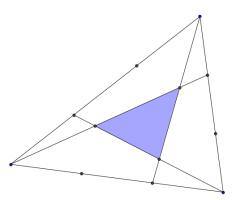
The three sides of this triangle have been split into three equal parts and three lines have been added.
What is the area of the smaller blue triangle as a fraction of the area of the original large triangle?
Show answer & extension
Hide answer & extension
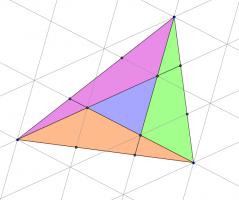
Draw on the following lines parallel to those which were added in the question.
Then a grid of copies of the smaller blue triangle has been created. Now consider the three triangles which are coloured green, purple and orange in the following diagram:
Each of these traingles covers half a parallelogram made from four blue triangles. Therefore the area of each of these triangles is twice the area of the small blue triangle.
And so the blue triangle covers one seventh of the large triangle.
Extension
If the sides of the triangle were split into \(n\) pieces the the lines added, what would the area of the smaller blue triangle be as a fraction of the area of the original large triangle?
![](javascript:showlimage("advent2021-isosceles.gif"))
![](javascript:showlimage("advent2020quads.png"))
![](javascript:showlimage("ad2020-ans-1.png"))
![](javascript:showlimage("circles-and-squares.png"))
![](javascript:showlimage("two triangles.png"))
![](javascript:showlimage("two-tri-ans1.png"))
![](javascript:showlimage("two-tri-ans2.png"))