Puzzles
9 December
The diagram below shows a rectangle. Two of its sides have been coloured blue. A red line has been drawn from two of its vertices to the midpoint of a side.
The total length of the blue lines is 50cm. The total length of the red lines is also 50cm. What is the area of the rectangle (in cm2)?
Show answer
Hide answer
Let \(a\) be the height of the rectangle. As the total of the blue lines is 50, the width of the rectangle is \(50-a\).
As the total of the red lines is 50, each red line segment is 25.
Using Pythagoras's theorem in one of the right-angled triangles, we see that:
$$a^2 + \left(\frac{50-a}{2}\right)^2 = 25^2$$
$$4a^2 + (50-a)^2 = 50^2$$
$$4a^2 + 50^2 - 100a + a^2 = 50^2$$
$$a(5a - 100) = 0$$
\(a\) is not zero, and so \(a=20\). This means that the area of the rectangle is 20×30=600.
20 December
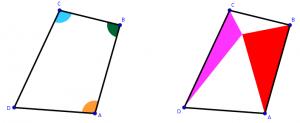
The diagram to the right shows (two copies of) quadrilateral ABCD.
The sum of the angles ABC and BCD (green and blue in quadrilateral on the left) is 180°.
The sum of the angles ABC and DAB (green and orange in quadrilateral on the left) is also 180°.
In the diagram on the right, a point inside the quadrilateral has been used to draw two triangles.
The area of the quadrilateral is 850. What is the smallest that the total area of the two triangles
could be?
Show answer
Hide answer
The angles adding up to 180° implies that AD and BC are parallel and AB and DC are parellel, and so the quadrilateral is a parallelogram.
The total area of the triangles will always be half the parallelogram, or 425.
10 December
A line is tangent to a curve if the line touches the curve at exactly one point.
The line \(y=-160\,000\) is tangent to the parabola \(y=x^2-ax\). What is \(a\)?
Show answer
Hide answer
A line \(y=\text{constant}\) that is tangent to a parabola must be a tangent to the minimum (or maximum) point.
\(y=x^2-ax\) can be rewritten as \(y=(x-a/2)^2-a^2/4\). The minimum of this will be at \(y=-a^2/4\).
If \(-a^2/4=-160\,000\), then \(a\) is 800.
7 December
What is the area of the largest triangle that fits inside a regular hexagon with area 952?
Show answer
Hide answer
The vertices of this triangle will be every other vertex of the hexagon: and other triangle can be made larger by moving one of its vertices closer to a vertex of the hexagon.
The area of this triangle is 476.
20 December
What is the area of the largest area triangle that has one side of length 32 and one side of length 19?
Show answer
Hide answer
The triangle will be largest when the two sides meet at a right angle. The area of this triangle is ½×32×19=304.
13 December
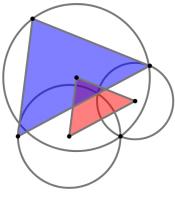
The diagram to the left shows three circles and two triangles. The three circles all meet at one point.
The vertices of the smaller red triangle are at the centres of the circles. The lines connecting the
vertices of the larger blue triangle to the point where all three circles meet are diameters of the
three circles.
The area of the smaller red triangle is 226. What is the area of the larger blue triangle?
Show answer
Hide answer
The two triangles are similar, and the sides of the blue triangle are twice the length of the red triangle. Therefore the area of the blue triangle
is 4 times the area of the red triangle. 226×4=904.
7 December
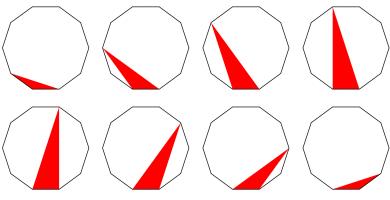
The picture below shows eight regular decagons. In each decagon, a red triangle has been drawn with vertices at three of the vertices of the decagon.
The area of each decagon is 240. What is the total area of all the red triangles?
Show answer
Hide answer
By rotating the triangles, they can be made to exactly cover the decagon.
The total area of all the triangles is therefore 240.
19 December
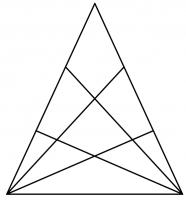
The diagram to the right shows a triangle. Two of the sides of the triangle have been split into three pieces, with lines drawn from the opposite vertex. In total, the diagram now contains 27 triangles of any size.
Another triangle has two of its sides split into eight pieces, with lines drawn from the opposite vertex. How many triangles (of any size) would this create?
Show answer
Hide answer
Each triangle must include one of the two corners at the base of the largest triangle (or both those corners).
To make triangles including the bottom left corner of the large triangle, we must pick two lines coming out of that corner, and one line coming out of the bottom right corner that is not the base of the triangle.
There are 9 lines coming out of the corners, so the total number of triangles is \(\left(\begin{array}{c}9\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=288\).
We now need to count the triangles that include the bottom right corner of the large triangle, but do not include both corners (as we've already counted thoses).
There are \(\left(\begin{array}{c}8\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=224\) ways to pick lines to make these triangles.
In total, this makes 512 triangles.