Puzzles
22 December
There are 4 ways to pick three vertices of a regular quadrilateral so that they form a right-angled triangle:
In another regular polygon with \(n\) sides, there are 14620 ways to pick three vertices so that they form a right-angled triangle. What is \(n\)?
Show answer
Hide answer
The vertices of any regular polygon lie on a circle, and so the three vertices we pick must lie on this circle. The triangle will be right-angled
if one of the edges of the triangle is a diameter of the circle.
If the regular polygon has \(n=2k\) sides, then there are \(k\) ways to pick two points that make a diameter, and \(2k-2\) ways to pick the third point to make the triangle, and so there are
a total of \(k(2k-2)=n(n-2)/2\) right-angled triangles. This means that we need to solve \(n(n-2)/2=14620\). The solution is \(n=172\), and so our polygon has 172 sides.
2 December
Today's number is the area of the largest dodecagon that it's possible to fit inside a circle with area \(\displaystyle\frac{172\pi}3\).
Cube multiples
Six different (strictly) positive integers are written on the faces of a cube. The sum of the numbers on any two adjacent faces is a multiple of 6.
What is the smallest possible sum of the six numbers?
Show answer & extension
Hide answer & extension
Consider the top, front, and right sides of the cube.
If the top number is \(a\) more than a multiple of six, then the front and right numbers must both be \(a\) less than a multiple of 6 (so that when added to the top number they make a multiple of 6). But when the front and right numbers are added, they make \(2a\) less than a multiple of 6; but this must also be a multiple of 6.
This is only possible if \(a=0\) or \(a=3\). So the numbers must be either all multiples of 6, or all 3 more than multiples of 6.
The smallest set of numbers that are all 3 more than multiples of 6 is 3,9,15,21,27,33. The sum of these is 108. The smallest set of numbers that are all multiples of 6 is the set with each number three more than these, so 108 is the smallest possible total.
Extension
Six numbers are written on the faces of a cube. The sum of the numbers on any two adjacent faces is a multiple of \(n\).
What is the smallest possible sum of the six numbers?
Polygraph
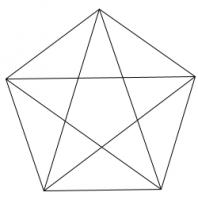
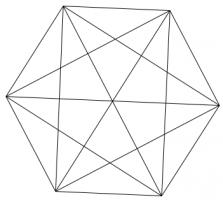
Draw a regular polygon. Connect all its vertices to every other vertex. For example, if you picked a pentagon or a hexagon, the result would look as follows:
Colour the regions of your shape so that no two regions which share an edge are the same colour. (Regions which only meet at one point can be the same colour.)
What is the least number of colours which this can be done with?
Show answer & extension
Hide answer & extension
It can be done with two colours. Let's call these red and blue.
Draw the polygon and colour it red. As each line is added to is, swap the colours on one side of the line which leaving them the same on the other side. At the end of this process you will have any polygon coloured with two colours.
Extension
How many regions will the regular shape be split into by the lines?