Advent calendar 2019
10 December
For all values of \(x\), the function \(f(x)=ax+b\) satisfies
$$8x-8-x^2\leqslant f(x)\leqslant x^2.$$
What is \(f(65)\)?
Edit: The left-hand quadratic originally said \(8-8x-x^2\). This was a typo and has now been corrected.
Show answer
Hide answer
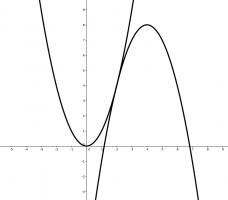
If we plot the two quadratics, we see that they meet at \(x=2\) where they both have gradient 4.
The line \(f(x)\) must therefore pass through the point \((2,4)\) and have gradient 4, so its equation is \(f(x)=4x-4\).
This means that \(f(65)\) is 256.
![](javascript:showlimage("advent2019quads.png"))