Advent calendar 2019
Advent 2019 logic puzzle
It's nearly Christmas and something terrible has happened: while out on a test flight, Santa's sled was damaged and Santa, Rudolph and Blitzen fell to the ground over the Advent Isles.
You need to find Santa and his reindeer before Christmas is ruined for everyone.
You have gathered one inhabitant of the four largest Advent Isles—Rum, Land, Moon and County—and they are going to give you a series of clues about where Santa and his reindeer landed.
However, one or more of the islanders you have gathered may have been involved in damaging Santa's sled and causing it to crash: any islander involved in this will lie to you to attempt to stop
you from finding Santa and his reindeer.
Once you are ready to search for Santa, Rudolph and Blitzen, you can find the map by following this link.
Each of the clues will be about Santa's, Rudolph's or Blitzen's positions in Advent Standard Coordinates (ASC): ASC are given by six two-digit numbers with dots inbetween, for example
12.52.12.13.84.55.
For this example coordinate, the islanders will refer to
(the first) 12 as the first coordinate,
52 as the second coordinate,
(the second) 12 as the third coordinate,
13 as the fourth coordinate,
84 as the fifth coordinate, and
55 as the sixth coordinate.
Here are the clues:
3
Rum says: "The product of all the digits in Blitzen's six coords is 432."21
Moon says: "Blitzen's fifth coord is 23."9
Moon says: "Blitzen's third coord is 23."1
Land says: "Santa's third coord ends in 3, 0 or 1."2
Land says: "Santa's third coord ends in 2, 0 or 3."4
Rum says: "Santa's second coord ends in 3, 4 or 1."12
Rum says: "Rudolph's second and sixth coords are both 64."10
Rum says: "All six of Rudolph's coords are factors of 256."18
Moon says: "Santa's fourth and fifth coords are both 79."24
County says: "Santa's third coord ends in 3, 2 or 1."22
Land says: "Santa's sixth coord is not 43."7
Rum says: "Santa's sixth coord is 43."23
County says: "One of the digits of Santa's third coord is 7."25
✔14
Land says: "Santa's third coord is 12."5
Rum says: "Santa's first coord is 36."15
Rum says: "Blitzen's first coord is 23."17
Rum says: "The first digit of Santa's third coord is 1."8
County says: "Santa's third coord shares a factor (≠1) with 270."6
County says: "Santa's second coord is 21."16
Land says: "Blitzen's second coord is 21."20
Moon says: "All six of Rudolph's coords are multiples of 8."11
Moon says: "The sum of Rudolph's six coords is 192."13
Moon says: "Santa's second coord is 21 or 11."19
Moon says: "Blitzen's fourth and sixth coords are both 11."To find a point's ASC coordinates, split a map of the islands into a 9×9 grid, then number the rows and columns 1 to 9: the first two digits of ASC give the vertical then horizontal position of a square in this grid.
The next two digits then give a smaller square when this square is then itself split into a 9×9 grid, and so on. An example is show below.
You can view the map here.
24 December
There are six 3-digit numbers with the property that the sum of their digits is equal to the product of their digits. Today's number is the largest of these numbers.
23 December
Arrange the digits 1-9 in a 3×3 square so the 3-digits numbers formed in the rows and columns are the types of numbers given at the ends of the rows and columns.
The number in the first column is today's number.
| a multiple of 4 | |||
| a cube | |||
| a multiple of 3 | |||
| today's number | a cube | an odd number |
22 December
In bases 3 to 9, the number 112 is:
\(11011_3\),
\(1300_4\),
\(422_5\),
\(304_6\),
\(220_7\),
\(160_8\), and
\(134_9\).
In bases 3, 4, 6, 8 and 9, these representations contain no digit 2.
There are two 3-digit numbers that contain no 2 in their representations in all the bases between 3 and 9 (inclusive). Today's number is the smaller of these two numbers.
21 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the smallest number you can make with the digits in the red boxes.
| + | - | = 7 | |||
| ÷ | - | ÷ | |||
| + | ÷ | = 8 | |||
| × | × | × | |||
| + | - | = 7 | |||
| = 12 | = 5 | = 28 |
20 December
The integers from 2 to 14 (including 2 and 14) are written on 13 cards (one number per card). You and a friend take it in turns to take one of the numbers.
When you have both taken five numbers, you notice that the product of the numbers you have collected is equal to the product of the numbers that your friend has collected.
What is the product of the numbers on the three cards that neither of you has taken?
19 December
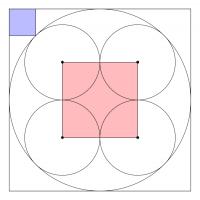
The diagram below shows three squares and five circles.
The four smaller circles are all the same size, and the red square's vertices are the centres of these circles.
The area of the blue square is 14 units. What is the area of the red square?
18 December
The final round of game show starts with £1,000,000. You and your opponent take it in turn to take any value between £1 and £900.
At the end of the round, whoever takes the final pound gets to take the money they have collected home, while the other player leaves with nothing.
You get to take an amount first. How much money should you take to be certain that you will not go home with nothing?
17 December
Eve picks a three digit number then reverses its digits to make a second number. The second number is larger than her original number.
Eve adds her two numbers together; the result is 584. What was Eve's original number?
16 December
Arrange the digits 1-9 in a 3×3 square so that:
the median number in the first row is 6;
the median number in the second row is 3;
the mean of the numbers in the third row is 4;
the mean of the numbers in the second column is 7;
the range of the numbers in the third column is 2,
The 3-digit number in the first column is today's number.
| median 6 | |||
| median 3 | |||
| mean 4 | |||
| today's number | mean 7 | range 2 |
15 December
There are 5 ways to make 30 by multiplying positive integers (including the trivial way):
- 30
- 2×15
- 3×10
- 5×6
- 2×3×5
Today's number is the number of ways of making 30030 by multiplying.
14 December
During one day, a digital clock shows times from 00:00 to 23:59. How many times during the day do the four digits shown on the clock add up to 14?
13 December
Each clue in this crossnumber (except 5A) gives a property of that answer that is true of no other answer. For example: 7A is a multiple of 13; but 1A, 3A, 5A, 1D, 2D, 4D, and 6D are all not multiples of 13.
No number starts with 0.
|
| ||||||||||||||||||||||||||||||||||||||||||||||
12 December
For a general election, the Advent isles are split into 650 constituencies. In each constituency, exactly 99 people vote: everyone votes for one of the two main parties: the Rum party or the
Land party. The party that receives the most votes in each constituency gets an MAP (Member of Advent Parliament) elected to parliament to represent that constituency.
In this year's election, exactly half of the 64350 total voters voted for the Rum party. What is the largest number of MAPs that the Rum party could have?
11 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10. Today's number is the product of the red digits.
| + | ÷ | = 2 | |||
| + | ÷ | ÷ | |||
| ÷ | ÷ | = 3 | |||
| ÷ | - | ÷ | |||
| ÷ | ÷ | = 1 | |||
| = 2 | = 1 | = 1 |
10 December
For all values of \(x\), the function \(f(x)=ax+b\) satisfies
$$8x-8-x^2\leqslant f(x)\leqslant x^2.$$
What is \(f(65)\)?
Edit: The left-hand quadratic originally said \(8-8x-x^2\). This was a typo and has now been corrected.
9 December
Arrange the digits 1-9 in a 3×3 square so that:
all the digits in the first row are odd;
all the digits in the second row are even;
all the digits in the third row are multiples of 3;
all the digits in the second column are (strictly) greater than 6;
all the digits in the third column are non-prime.
The number in the first column is today's number.
| all odd | |||
| all even | |||
| all multiples of 3 | |||
| today's number | all >6 | all non-prime |
8 December
Carol uses the digits from 0 to 9 (inclusive) exactly once each to write five 2-digit even numbers, then finds their sum. What is the largest number she could have obtained?
7 December
The sum of the coefficients in the expansion of \((x+1)^5\) is 32. Today's number is the sum of the coefficients in the expansion of \((2x+1)^5\).
6 December
Noel's grandchildren were in born in November in consecutive years. Each year for Christmas, Noel gives each of his grandchildren their age in pounds.
Last year, Noel gave his grandchildren a total of £208. How much will he give them in total this year?
5 December
28 points are spaced equally around the circumference of a circle. There are 3276 ways to pick three of these points.
The three picked points can be connected to form a triangle. Today's number is the number of these triangles that are isosceles.
4 December
There are 5 ways to tile a 3×2 rectangle with 2×2 squares and 2×1 dominos.
Today's number is the number of ways to tile a 9×2 rectangle with 2×2 squares and 2×1 dominos.
3 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number you can make with the digits in the red boxes.
| + | + | = 21 | |||
| + | × | × | |||
| + | + | = 10 | |||
| + | ÷ | × | |||
| + | + | = 14 | |||
| = 21 | = 10 | = 14 |
2 December
You have 15 sticks of length 1cm, 2cm, ..., 15cm (one of each length). How many triangles can you make by picking three sticks and joining their ends?
Note: Three sticks (eg 1, 2 and 3) lying on top of each other does not count as a triangle.
Note: Rotations and reflections are counted as the same triangle.
1 December
If you write out the numbers from 1 to 1000 (inclusive), how many times will you write the digit 1?