Blog
2019-07-03
This year's Big Internet Math-Off
is now underway with 15 completely new contestants (plus one returning contender). As I'm not the returning contestant, I haven't been spending
my time preparing my pitches. Instead, I've spent my time making an
unofficial Big Internet Math-Off sticker book.
To complete the sticker book, you will need to collect 162 different stickers. Every day, you will be given a pack of 5 stickers; there are
also some bonus packs available if you can find them (Hint: keep reading).
How many stickers will I need?
Using the same method as I did for last year's World Cup sticker book,
you can work out that the expected number of stickers needed to finish the sticker book:
If you have already stuck \(n\) stickers into your album, then the probability that the next sticker you get is new is
$$\frac{162-n}{162}.$$
The probability that the second sticker you get is the next new sticker is
$$\mathbb{P}(\text{next sticker is not new})\times\mathbb{P}(\text{sticker after next is new})$$
$$=\frac{n}{162}\times\frac{162-n}{162}.$$
Following the same method, we can see that the probability that the \(i\)th sticker you buy is the next new sticker is
$$\left(\frac{n}{162}\right)^{i-1}\times\frac{162-n}{162}.$$
Using this, we can calculate the expected number of stickers you will need to buy until you find a new one:
$$\sum_{i=1}^{\infty}i \left(\frac{162-n}{162}\right) \left(\frac{n}{162}\right)^{i-1} = \frac{162}{162-n}$$
Therefore, to get all 162 stickers, you should expect to buy
$$\sum_{n=0}^{161}\frac{162}{162-n} = 918 \text{ stickers}.$$
Using just your daily packs, it will take you until the end of the year to collect this many stickers.
Of course, you'll only need to collect this many if you don't swap your duplicate stickers.
How many stickers will I need if I swap?
To work out the expected number of stickers stickers you'd need if you swap, let's first think about two people who want to complete
their stickerbooks together. If there are \(a\) stickers that both collectors need and \(b\) stickers that one collector has and the other one
needs, then let \(E_{a,b}\) be the expected number of stickers they need to finish their sticker books.
The next sticker they get could be one of three things:
- A sticker they both need (with probability \(\frac{a}{162}\));
- A sticker one of them needs (with probability \(\frac{b}{162}\));
- A sticker they both have (with probability \(\frac{162-a-b}{162}\)).
Therefore, the expected number of stickers they need to complete their sticker books is
$$E_{a,b}=1+\frac{a}{162}E_{a-1,b+1}+\frac{b}{162}E_{a,b-1}+\frac{162-a-b}{162}E_{a,b}.$$
This can be rearranged to give
$$E_{a,b}=
\frac{162}{a+b}+
\frac{a}{a+b}E_{a-1,b+1}
+\frac{b}{a+b}E_{a,b-1}
$$
We know that $E_{0,0}=0$ (as if \(a=0\) and \(b=0\), both collectors have already finished their sticker books). Using this and the
formula above, we can work out that
$$E_{0,1}=162+E_{0,0}=162$$
$$E_{1,0}=162+E_{0,1}=324$$
$$E_{0,2}=\frac{162}2+E_{0,1}=243$$
$$E_{1,1}=\frac{162}2+\frac12E_{0,2}+\frac12E_{1,0}=364.5$$
... and so on until we find that \(E_{162,0}=1269\), and so our collectors should expect to collect 634 stickers each to complete their
sticker books.
For three people, we can work out that if there are \(a\) stickers that all three need, \(b\) stickers that two need, and \(c\) stickers
that one needs, then
$$
E_{a,b,c}
= \frac{162}{a+b+c}+
\frac{a}{a+b+c}E_{a-1,b+1,c}
+\frac{b}{a+b+c}E_{a,b-1,c+1}
+\frac{c}{a+b+c}E_{a,b,c-1}.
$$
In the same way as for two people, we find that \(E_{162,0,0}=1572\), and so our collectors should expect to collect 524 stickers each
to complete their sticker books.
Doing the same thing for four people gives an expected 463 stickers required each.
After four people, however, the Python code I wrote to do these calculations takes too long to run, so instead I approximated the numbers
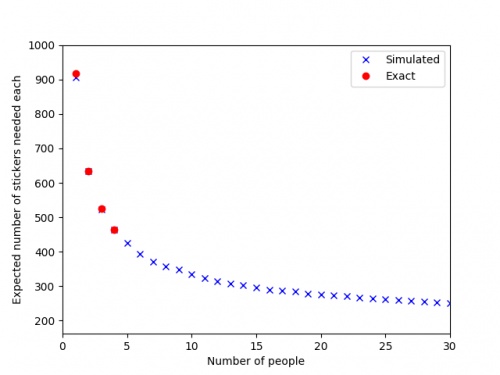
by simulating 500 groups of \(n\) people collecting stickers, and taking the average number of stickers they needed. The results are shown in
the graph below.
The red dots are the expected values we calculated exactly, and the blue crosses are the simulated values.
It looks like you'll need to collect at least 250 stickers to finish the album: in order to get this many before the end of the Math-Off,
you'll need to find 20 bonus packs...
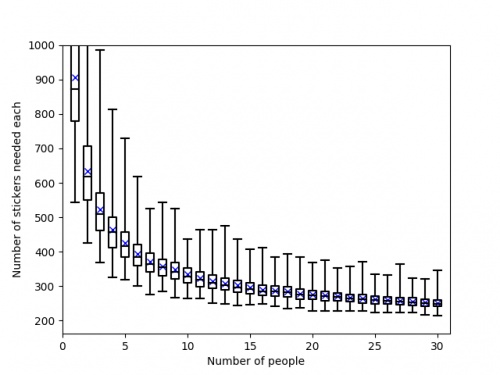
Of course, these are just the mean values and you could get lucky and need fewer stickers. The next graph shows box plots with the
quartiles of the data from the simulations.
So if you're lucky, you could complete the album with fewer stickers or fewer friends.
As a thank you for reading to the end of this blog post, here's a link that
will give you two bonus packs and help you on your way to the 250 expected stickers...
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2019-07-06
@Pat Ashforth: Thanks, fixedMatthew
Link to sticker book, in the first paragraph, does not work. It points to mathoffstickbook.com
Pat Ashforth
minor typo for the 2 collector case
> and so our collectors should expect to collect 364 stickers
should be 634.
> and so our collectors should expect to collect 364 stickers
should be 634.
Road
Add a Comment
2019-06-19
A308092 The sum of the first \(n\) terms of the sequence is the concatenation of the first \(n\) bits of the sequence read as binary, with \(a(1) = 1\).1, 2, 3, 7, 14, 28, 56, 112, 224, 448, 896, 1791, 3583, 7166, ...

To understand this definition, let's look at the first few terms of this sequence written in binary:
By "the concatenation of the first \(n\) bits of the sequence", it means the first \(n\) binary digits of the whole sequence written in order:
1, then 11, then 110, then 1101, then 11011, then 110111, and so on. So the definition means:
- The first term is 1, as given in the definition (\(a(1)=1\)).
- The sum of the first 2 terms is the first 2 digits: \(1+10=11\).
- The sum of the first 3 terms is the first 3 digits: \(1+10+11=110\).
- The sum of the first 4 terms is the first 4 digits: \(1+10+11+111=1101\).
- The sum of the first 5 terms is the first 5 digits: \(1+10+11+111+1110=11011\).
As we know that the sum of the first \(n-1\) terms is the first \(n-1\) digits, we can calculate the third term of this sequence onwards using:
"\(a(n)\) is the concatenation of the first \(n\) bits of the sequence subtract concatenation of the first \(n-1\) bits of the sequence":
- The third term is \(110 - 11 = 11\).
- The fourth term is \(1101 - 110 = 111\).
- The fourth term is \(11011 - 1101 = 1110\).
- The fifth term is \(110111 - 11011 = 11100\).
The conjecture
Peter's conjecture is that the number of 1s in each term is greater than or equal to the number of 1s in the previous term.
I'm going to prove this conjecture. If you'd like to have a try first, stop reading now and come back when you're ready for spoilers.
(If you'd like a hint, read the next section then pause again.)
Adding a digit
The third term of the sequence onwards can be calculated by subtracting the first \(n-1\) digits from the first \(n\) digits.
If the first \(n-1\) digits form a binary number \(x\), then the first \(n\) digits will be \(2x+d\), where \(d\) is the \(n\)th digit
(because moving all the digits to the left one place in binary is multiplying by two).
Therefore the different is \(2x+d-x=x+d\), and so we can work out the \(n\)th term of the sequence by adding the \(n\)th digit in the
sequence to the first \(n-1\) digits. (Hat tip to Martin Harris, who spotted this first.)
Carrying
Adding 1 to a binary number the ends in 1 will cause 1 to carry over to the left. This carrying will continue until the 1 is carried into
a position containing 0, and after this all the digits to the left of this 0 will remain unchanged.
Therefore adding a digit to
the first \(n-1\) digits can only change the digits from the rightmost 0 onwards.
Endings
We can therefore disregard all the digits before the rightmost 0, and look at how the \(n\)th term compares to the \((n-1)\)th term.
There are 5 ways in which the first \(n\) digits could end:
- \(00\)
- \(010\)
- \(01...10\) (where \(1...1\) is a string of 2 or more ones)
- \(01\)
- \(01...1\) (where \(1...1\) is again a string of 2 or more ones)
We now look at each of these in turn and show that the \(n\)th term will contain at least as many ones at the \((n-1)\)th term.
Case 1: \(00\)
If the first \(n\) digits of the sequence are \(x00\) (a binary number \(x\) followed by two zeros), then the \((n-1)\)th term of the
sequence is \(x+0=x\), and the \(n\)th term of the sequence is \(x0+0=x0\). Both \(x\) and \(x0\) contain the same number of ones.
Case 2: \(010\)
If the first \(n\) digits of the sequence are \(x010\), then the \((n-1)\)th term of the sequence is \(x0+1=x1\),
and the \(n\)th term of the sequence is \(x01+0=x01\). Both \(x1\) and \(x01\) contain the same number of ones.
Case 3: \(01...10\)
If the first \(n\) digits of the sequence are \(x01...10\), then the \((n-1)\)th term of the sequence is \(x01...1+1=x10...0\),
and the \(n\)th term of the sequence is \(x01...10+1=x01...1\). \(x01...1\) contains more ones than \(x10...0\).
Case 4: \(01\)
If the first \(n\) digits of the sequence are \(x01\), then the \((n-1)\)th term of the sequence is \(x+0=x\),
and the \(n\)th term of the sequence is \(x0+1=x1\). \(x1\) contains one more one than \(x\).
Case 5: \(01...1\)
If the first \(n\) digits of the sequence are \(x01...1\), then the \((n-1)\)th term of the sequence is \(x01...1+1=x10...0\),
and the \(n\)th term of the sequence is \(x01...1+1=x10...0\). Both these contain the same number of ones.
In all five cases, the \(n\)th term contains more ones or an equal number of ones to the \((n-1)\)th term, and so the conjecture is true.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2019-04-09
In the latest issue of Chalkdust,
I wrote an article
with Edmund Harriss about the Harriss spiral that appears on the cover of the magazine.
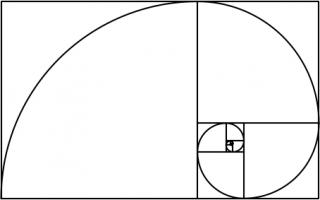
To draw a Harriss spiral, start with a rectangle whose side lengths are in the plastic ratio; that is the ratio \(1:\rho\)
where \(\rho\) is the real solution of the equation \(x^3=x+1\), approximately 1.3247179.
This rectangle can be split into a square and two rectangles similar to the original rectangle. These smaller rectangles can then be split up in the same manner.
Drawing two curves in each square gives the Harriss spiral.
This spiral was inspired by the golden spiral, which is drawn in a rectangle whose side lengths are in the golden ratio of \(1:\phi\),
where \(\phi\) is the positive solution of the equation \(x^2=x+1\) (approximately 1.6180339). This rectangle can be split into a square and one
similar rectangle. Drawing one arc in each square gives a golden spiral.
The golden and Harriss spirals are both drawn in rectangles that can be split into a square and one or two similar rectangles.
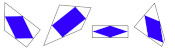
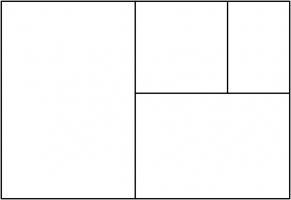
Continuing the pattern of these arrangements suggests the following rectangle, split into a square and three similar rectangles:
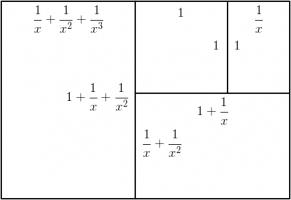
Let the side of the square be 1 unit, and let each rectangle have sides in the ratio \(1:x\). We can then calculate that the lengths of
the sides of each rectangle are as shown in the following diagram.
The side lengths of the large rectangle are \(\frac{1}{x^3}+\frac{1}{x^2}+\frac2x+1\) and \(\frac1{x^2}+\frac1x+1\). We want these to also
be in the ratio \(1:x\). Therefore the following equation must hold:
$$\frac{1}{x^3}+\frac{1}{x^2}+\frac2x+1=x\left(\frac1{x^2}+\frac1x+1\right)$$
Rearranging this gives:
$$x^4-x^2-x-1=0$$
$$(x+1)(x^3-x^2-1)=0$$
This has one positive real solution:
$$x=\frac13\left(
1
+\sqrt[3]{\tfrac12(29-3\sqrt{93})}
+\sqrt[3]{\tfrac12(29+3\sqrt{93})}
\right).$$
This is equal to 1.4655712... Drawing three arcs in each square allows us to make a spiral from a rectangle with sides in this ratio:
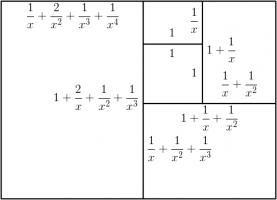
Adding a fourth rectangle leads to the following rectangle.
The side lengths of the largest rectangle are \(1+\frac2x+\frac3{x^2}+\frac1{x^3}+\frac1{x^4}\) and \(1+\frac2x+\frac1{x^2}+\frac1{x^3}\).
Looking for the largest rectangle to also be in the ratio \(1:x\) leads to the equation:
$$1+\frac2x+\frac3{x^2}+\frac1{x^3}+\frac1{x^4} = x\left(1+\frac2x+\frac1{x^2}+\frac1{x^3}\right)$$
$$x^5+x^4-x^3-2x^2-x-1 = 0$$
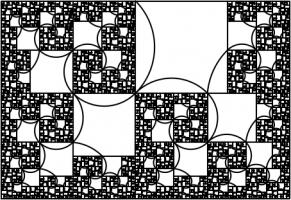
This has one real solution, 1.3910491... Although for this rectangle, it's not obvious which arcs to draw to make a
spiral (or maybe not possible to do it at all). But at least you get a pretty fractal:
We could, of course, continue the pattern by repeatedly adding more rectangles. If we do this, we get the following polynomials
and solutions:
| Number of rectangles | Polynomial | Solution |
| 1 | \(x^2 - x - 1=0\) | 1.618033988749895 |
| 2 | \(x^3 - x - 1=0\) | 1.324717957244746 |
| 3 | \(x^4 - x^2 - x - 1=0\) | 1.465571231876768 |
| 4 | \(x^5 + x^4 - x^3 - 2x^2 - x - 1=0\) | 1.391049107172349 |
| 5 | \(x^6 + x^5 - 2x^3 - 3x^2 - x - 1=0\) | 1.426608021669601 |
| 6 | \(x^7 + 2x^6 - 2x^4 - 3x^3 - 4x^2 - x - 1=0\) | 1.4082770325090774 |
| 7 | \(x^8 + 2x^7 + 2x^6 - 2x^5 - 5x^4 - 4x^3 - 5x^2 - x - 1=0\) | 1.4172584399350432 |
| 8 | \(x^9 + 3x^8 + 2x^7 - 5x^5 - 9x^4 - 5x^3 - 6x^2 - x - 1=0\) | 1.412713760332943 |
| 9 | \(x^{10} + 3x^9 + 5x^8 - 5x^6 - 9x^5 - 14x^4 - 6x^3 - 7x^2 - x - 1=0\) | 1.414969877544769 |
The numbers in this table appear to be heading towards around 1.414, or \(\sqrt2\).
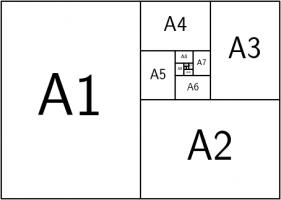
This shouldn't come as too much of a surprise because \(1:\sqrt2\) is the ratio of the sides of A\(n\) paper (for \(n=0,1,2,...\)).
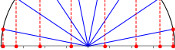
A0 paper can be split up like this:
This is a way of splitting up a \(1:\sqrt{2}\) rectangle into an infinite number of similar rectangles, arranged following the pattern,
so it makes sense that the ratios converge to this.
Other patterns
In this post, we've only looked at splitting up rectangles into squares and similar rectangles following a particular pattern. Thinking about
other arrangements leads to the following question:
Given two real numbers \(a\) and \(b\), when is it possible to split an \(a:b\) rectangle into squares and \(a:b\) rectangles?
If I get anywhere with this question, I'll post it here. Feel free to post your ideas in the comments below.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@g0mrb: CORRECTION: There seems to be no way to correct the glaring error in that comment. A senior moment enabled me to reverse the nomenclature for paper sizes. Please read the suffixes as (n+1), (n+2), etc.
(anonymous)
I shall remain happy in the knowledge that you have shown graphically how an A(n) sheet, which is 2 x A(n-1) rectangles, is also equal to the infinite series : A(n-1) + A(n-2) + A(n-3) + A(n-4) + ... Thank-you, and best wishes for your search for the answer to your question.
g0mrb
Add a Comment
2019-03-26
I originally wrote this post for The Aperiodical.
A few months ago, Adam Townsend went to lunch and had a conversation. I wasn't there, but I imagine the conversation went something like this:
Adam: Hello.Smitha: Hello.Adam: How are you?Smitha: Not bad. I've had a funny idea, actually.Adam: Yes?Smitha: You know how the \hat command in LaTeΧ puts a caret above a letter?... Well I was thinking it would be funny if someone made a package that made the \hat command put a picture of an actual hat on the symbol instead?Adam: (After a few hours of laughter.) I'll see what my flatmate is up to this weekend...Jeff: What on Earth are you two talking about?!

As anyone who has been anywhere near maths at a university in the last ∞ years will be able to tell you,
LaTeΧ is a piece of maths typesetting software. It's a bit like a version of Word that runs in terminal and makes PDFs with really
pretty equations.
By default, LaTeΧ can't do very much, but features can easily added by importing packages: importing the graphicsx
package allows you to put images in your PDF; importing geometry allows you to easily change the page margins; and importing
realhats makes the \hat command put real hats above symbols.
Changing the behaviour of \hat
By default, the LaTeΧ command \hat puts a pointy "hat" above a symbol:
After Adam's conversation, we had a go at redefining the \hat command by putting the following
at the top of our LaTeΧ file.
LaTeΧ
\renewcommand{\hat}[1]{% We put our new definition here
}
After a fair amount of fiddling with the code, we eventually got it to produce the following result:
We were now ready to put our code into a package so others could use it.
How to write a package
A LaTeΧ package is made up of:
- a sty file, containing a collection of commands like the one we wrote above;
- a PDF of documentation showing users how to use your package;
- a README file with a basic description of your package.
It's quite common to make the first two of these by making a
dtx file
and an ins file. And no, we have
no idea either why these are the file extensions used or why this is supposedly simpler than making a sty file and a PDF.
The ins file says which bits of the dtx should be used to make up the sty file.
Our ins file looks like this:
LaTeΧ
\input{docstrip.tex}\keepsilent
\usedir{tex/latex/realhats}
\preamble
*License goes here*
\endpreamble
\askforoverwritefalse
\generate{
\file{realhats.sty}{\from{realhats.dtx}{realhats}}
}
\endbatchfile
The most important command in this file is \generate: this says that that the file
realhats.sty should be made from the file realhats.dtx
taking all the lines that are marked as part of realhats. The following is part of our dtx file:
LaTeΧ
%\lstinline{realhats} is a package for \LaTeX{} that makes the \lstinline{\hat}%command put real hats on symbols.
%For example, the input \lstinline@\hat{a}=\hat{b}@ will produce the output:
%\[\hat{a}=\hat{b}\]
%To make a vector with a hat, the input \lstinline@\hat{\mathbf{a}}@ produces:
%\[\hat{\mathbf{a}}\]
%
%\iffalse
%<*documentation>
\documentclass{article}
\usepackage{realhats}
\usepackage{doc}
\usepackage{listings}
\title{realhats}
\author{Matthew W.~Scroggs \& Adam K.~Townsend}
\begin{document}
\maketitle
\DocInput{realhats.dtx}
\end{document}
%</documentation>
%\fi
%\iffalse
%<*realhats>
\NeedsTeXFormat{LaTeX2e}
\ProvidesPackage{realhats}[2019/02/02 realhats]
\RequirePackage{amsmath}
\RequirePackage{graphicx}
\RequirePackage{ifthen}
\renewcommand{\hat}[1]{
% We put our new definition here
}
%</realhats>
%\fi
The lines near the end between <*realhats>
and </realhats> will be included in the sty file, as they are marked at part of
realhats.
The rest of this file will make the PDF documentation when the dtx file is compiled.
The command \DocInput tells LaTeΧ to include the dtx again, but with the
%s that make lines into comments removed. In this way all the comments that describe the functionality will end up
in the PDF. The lines that define the package will not be included in the PDF as they are between \iffalse and
\fi.
Writing both the commands and the documentation in the same file like this means that the resulting file is quite a mess, and really quite
ugly. But this is apparently the standard way of writing LaTeΧ packages, so rest assured that it's not just our code that ugly and
confusing.
What to do with your package
Once you've written a package, you'll want to get it out there for other people to use. After all, what's the point of being able to
put real hats on top of symbols if the whole world can't do the same?
First, we put the source code of our package on GitHub, so that Adam and I had an
easy way to both work on the same code. This also allows other LaTeΧ lovers to see the source and contribute to it, although none have
chosen to add anything yet.
Next, we submitted our package to CTAN, the Comprehensive TeΧ Archive Network.
CTAN is an archive of thousands of LaTeΧ packages, and putting realhats there gives LaTeΧ users
everywhere easy access to real hats. Within days of being added to CTAN, realhats was added (with no work by us)
to MikTeX and TeX Live
to allow anyone using these LaTeΧ distributions to seemlessly install it as soon as it is needed.
We figured that the packaged needed a website too, so we made one. We also figured that the website
should look as horrid as possible.
How to use realhats
So if you want to end fake hats and put real hats on top of your symbols, you can simply write \usepackage{realhats}
at the top of your LaTeΧ file.

realhats: gotta put them all in academic papers
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
I am a pensioner studying maths with OU. Currently doing M248 stats module. My enjoyment of MLEs has been magnified by your wonderful realhats package. It's a good job I'm 99% tee-total or my tutor would be getting a dubious assignment (still leaves a 1% chance of malt-driven mischief though).
Dave
Add a Comment
2019-01-01
It's 2019, and the Advent calendar has disappeared, so it's time to reveal the answers and annouce the winners.
But first, some good news: with your help, Santa was able to work out who had stolen the presents and save Christmas:
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar, reveal the solution and a couple of notes and Easter eggs.
Highlights
My first highlight is the first puzzle in the calendar. This is one of my favourites as it has a pleasingly neat solution involving a
surprise appearance of a very famous sequence.
1 December
There are 5 ways to write 4 as the sum of 1s and 2s:
- 1+1+1+1
- 2+1+1
- 1+2+1
- 1+1+2
- 2+2
Today's number is the number of ways you can write 12 as the sum of 1s and 2s.
My next highlight is a puzzle that I was particularly proud of cooking up: again, this puzzle at first glance seems like it'll take a
lot of brute force to solve, but has a surprisingly neat solution.
10 December
The equation \(x^2+1512x+414720=0\) has two integer solutions.
Today's number is the number of (positive or negative) integers \(b\) such that \(x^2+bx+414720=0\) has two integer solutions.
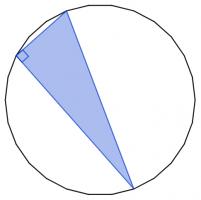
My next highlight is a geometry problem that appears to be about polygons, but actually it's about a secret circle.
12 December
There are 2600 different ways to pick three vertices of a regular 26-sided shape. Sometimes the three vertices you pick form a right angled triangle.
Today's number is the number of different ways to pick three vertices of a regular 26-sided shape so that the three vertices make a right angled triangle.
My final highlight is a puzzle about the expansion of a fraction in different bases.
22 December
In base 2, 1/24 is
0.0000101010101010101010101010...
In base 3, 1/24 is
0.0010101010101010101010101010...
In base 4, 1/24 is
0.0022222222222222222222222222...
In base 5, 1/24 is
0.0101010101010101010101010101...
In base 6, 1/24 is
0.013.
Therefore base 6 is the lowest base in which 1/24 has a finite number of digits.
Today's number is the smallest base in which 1/10890 has a finite number of digits.
Note: 1/24 always represents 1 divided by twenty-four (ie the 24 is written in decimal).
Notes and Easter eggs
I had a lot of fun this year coming up with the names for the possible theives. In order to sensibly colour code each suspect's clues,
there is a name of a colour hidden within each name:
Fred Metcalfe,
Jo Ranger,
Bob Luey,
Meg Reeny, and
Kip Urples.
Fred Metcalfe's colour is contained entirely within his forename, so you may be wondering
where his surname came from. His surname is shared with Paul Metcalfe—the real name of a captain whose codename was a certain shade of red.
On 20 December, Elijah Kuhn emailed me to point out that it was possible to solve the final puzzle a few days early: although he could not yet work
out the full details of everyone's timetable, he had enough information to correctly work out who the culprit was and between which times the theft
had taken place.
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. This year, I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
You can see that the most difficult puzzles were those on
13,
24, and
10 December;
and the easiest puzzles were on
5,
23,
11, and
15 December.
I also snuck a small Easter egg into the door arrangement: the doors were arranged to make a magic square, with each row and column, plus the two diagonals, adding to 55.
The solutions to all the individual puzzles can be found here. Using the clues, you can work out that everyone's seven activities
formed the following timetable.
| Bob Luey | Fred Metcalfe | Jo Ranger | Kip Urples | Meg Reeny |
| 0:00–1:21 Billiards | 0:00–2:52 Maths puzzles | 0:00–2:33 Maths puzzles | 0:00–1:21 Billiards | 0:00–1:10 Ice skating |
| 1:10–2:33 Skiing | ||||
| 1:21–2:52 Ice skating | 1:21–2:52 Stealing presents | |||
| 2:33–4:45 Billiards | 2:33–4:45 Billiards | |||
| 2:52–3:30 Lunch | 2:52–3:30 Lunch | 2:52–3:30 Lunch | ||
| 3:30–4:45 Climbing | 3:30–4:45 Climbing | 3:30–4:45 Climbing | ||
| 4:45–5:42 Curling | 4:45–5:42 Curling | 4:45–5:42 Curling | 4:45–5:42 Curling | 4:45–5:42 Lunch |
| 5:42–7:30 Maths puzzles | 5:42–7:30 Ice skating | 5:42–7:30 Chess | 5:42–7:30 Chess | 5:42–7:30 Maths puzzles |
| 7:30–10:00 Skiing | 7:30–9:45 Chess | 7:30–8:45 Skiing | 7:30–10:00 Maths puzzles | 7:30–9:45 Chess |
| 8:45–9:45 Lunch | ||||
| 9:45–10:00 Table tennis | 9:45–10:00 Table tennis | 9:45–10:00 Table tennis | ||
Following your investigation, Santa found all the presents hidden under Kip Urples's bed, fired Kip and sucessfully delivered all the presents
on Christmas Eve.
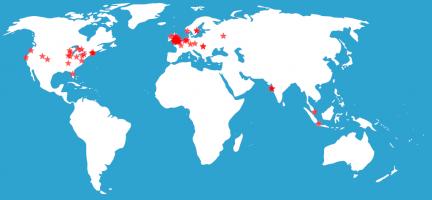
The winners
And finally (and maybe most importantly), on to the winners: 73 people submitted answers to the final logic puzzle. Their (very) approximate locations are shown on this map:
From the correct answers, the following 10 winners were selected:
| 1 | Sarah Brook |
| 2 | Mihai Zsisku |
| 3 | Bhavik Mehta |
| 4 | Peter Byrne |
| 5 | Martin Harris |
| 6 | Gert-Jan de Vries |
| 7 | Lyra |
| 8 | James O'Driscoll |
| 9 | Harry Poole |
| 10 | Albert Wood |
Congratulations! Your prizes will be on their way shortly. Additionally, well done to
Alan Buck, Alex Ayres, Alex Bolton, Alex Lam, Alexander Ignatenkov, Alexandra Seceleanu, Andrew Turner, Ashwin Agarwal,
Becky Russell, Ben Reiniger, Brennan Dolson,
Carl Westerlund, Cheng Wai Koo, Christopher Embrey, Corbin Groothuis,
Dan Whitman, David, David Ault, David Kendel, Dennis Oltmanns,
Elijah Kuhn, Eric, Eric Kolbusz, Evan Louis Robinson,
Felix Breton, Fred Verheul,
Gregory Loges,
Hannah,
Jean-Noël Monette, Jessica Marsh, Joe Gage, Jon Palin, Jonathan Winfield,
Kai Lam,
Louis de Mendonca,
M Oostrom, Martine Vijn Nome, Matt Hutton, Matthew S, Matthew Wales, Michael DeLyser, MikeKim,
Naomi Bowler,
Pranshu Gaba,
Rachel Bentley, Raymond Arndorfer, Rick Simineo, Roni, Rosie Paterson,
Sam Hartburn, Scott, Sheby, Shivanshi, Stephen Cappella, Steve Paget,
Thomas Smith, Tony Mann,
Valentin Vălciu, Yasha Ayyari, Zack Wolske, and Zoe Griffiths, who all also submitted the correct answer but were too unlucky to win prizes
this time.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment